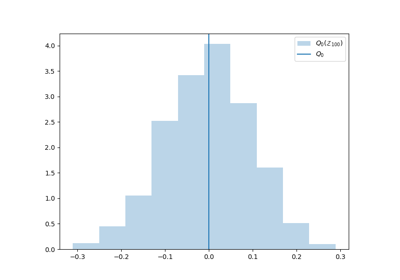
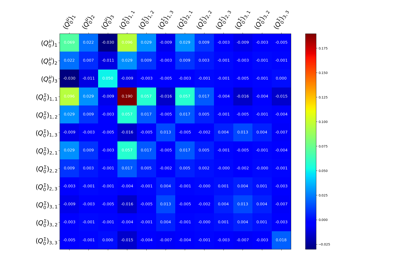
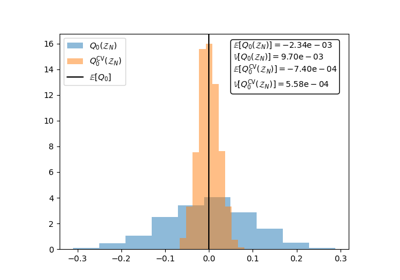
Theoretical Tutorials
Below is a gallery of tutorials providing detailed mathematical background on the methods in PyApprox.
This tutorials provide more detail than the set of examples found here which simply show how to use different methods with the least amount of code.
Model Analysis
Below are tutorials on various model analysis techniques
Inference
Below is a gallery of foundational tutorials probabilistic inversion
Experimental Design
The next release will contain a gallery of foundational tutorials on experimental design
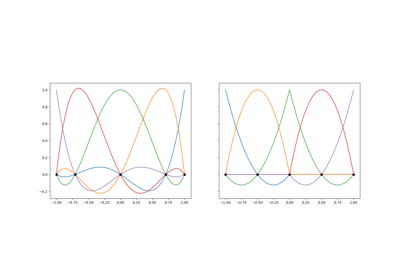
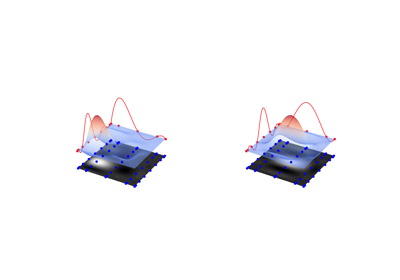
Surrogates
Multi-Fidelity Methods
Multi-fidelity methods utilize an ensemble of models, enriching a small number of high-fidelity simulations with larger numbers of simulations from models of varying prediction accuracy and reduced cost, to enable greater exploration and resolution of uncertainty while maintaining deterministic prediction accuracy. The effectiveness of multi-fidelity approaches depends on the ability to identify and exploit relationships among models within the ensemble.
The relationships among models within a model ensemble vary greatly, and most existing approaches focus on exploiting a specific type of structure for a presumed model sequence. For example, [KOB2000], [LGIJUQ2014], [NGXSISC2014], [TJWGSIAMUQ2015] build surrogate approximations that leverage a 1D hierarchy of models of increasing fidelity, with varying physics and/or numerical discretizations. While Multi-index collocation [HNTTCMAME2016] leverage a multi-dimensional hierarchy controlled my two or more numerical discretization hyper-parameters. Similary [CGSTCVS2011], [GOR2008] exploit a 1D hierarchy of models to estimate statistics such as mean and variance using Monte Carlo methods.
This gallery of tutorials discusses the most popular multi-fidelity methods for quantifying uncertainty in complex models.

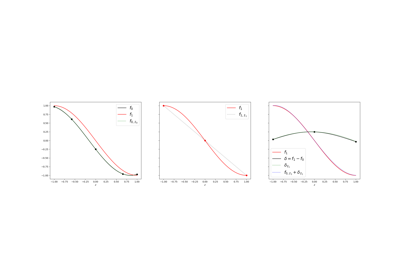
Delta-Based Covariance Formulas For Approximate Control Variates
Parametrically Defined Approximate Control Variates
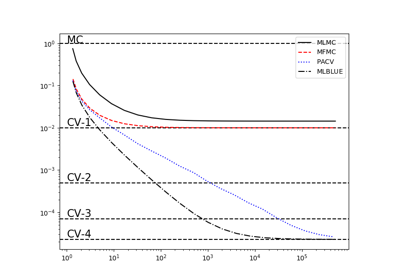
Multilevel Best Linear Unbiased estimators (MLBLUE)