Monte Carlo Quadrature

This tutorial describes how to use Monte Carlo sampling to compute the expectations of the output of a model \(f(\rv):\reals^{D}\to\reals\) parameterized by a set of variables \(\rv=[\rv_1,\ldots,\rv_D]^\top\) with joint density given by \(\rho(\rv):\reals^{d}\to\reals\). Specifically, our goal is to approximate the integral

\[Q=\int_\rvdom f(\rv)\pdf(\rv)\dx{\rv}\]

using Monte Carlo quadrature applied to an approximation \(f_\alpha\) of the function \(f\), e.g. a representing a finite element approximation to the solution of a set of governing equations, where \(\alpha\) is contols the accuracy of the approximation.

Monte Carlo quadrature approximates the integral

\[Q_\alpha=\int_\rvdom f_\alpha(\rv)\pdf(\rv)\dx{\rv}\approx Q\]

by drawing \(N\) random samples \(\rvset_N\) of \(\rv\) from \(\pdf\) and evaluating the function at each of these samples to obtain the data pairs \(\{(\rv^{(n)},f^{(n)}_\alpha)\}_{n=1}^N\), where \(f^{(n)}_\alpha=f_\alpha(\rv^{(n)})\) and computing

\[Q_{\alpha}(\rvset_N)=N^{-1}\sum_{n=1}^N f^{(n)}_\alpha\]

This estimate of the mean,is itself a random quantity, which we call an estimator, because its value depends on the \(\rvset_N\) realizations of the inputs \(\rvset_N\) used to compute \(Q_{\alpha}(\rvset_N)\). Specifically, using two different sets \(\rvset_N\) will produce to different values.

To demonstrate this phenomenon, we will estimate the mean of a simple algebraic function \(f_0\) which belongs to an ensemble of models

\[\begin{split}f_0(\rv) &= A_0 \left(\rv_1^5\cos\theta_0 +\rv_2^5\sin\theta_0\right), \\ f_1(\rv) &= A_1 \left(\rv_1^3\cos\theta_1 +\rv_2^3\sin\theta_1\right)+s_1,\\ f_2(\rv) &= A_2 \left(\rv_1 \cos\theta_2 +\rv_2 \sin\theta_2\right)+s_2\end{split}\]

where \(\rv_1,\rv_2\sim\mathcal{U}(-1,1)\) and all \(A\) and \(\theta\) coefficients are real. We choose to set \(A=\sqrt{11}\), \(A_1=\sqrt{7}\) and \(A_2=\sqrt{3}\) to obtain unitary variance for each model. The parameters \(s_1,s_2\) control the bias between the models. Here we set \(s_1=1/10,s_2=1/5\). Similarly we can change the correlation between the models in a systematic way (by varying \(\theta_1\). We will levarage this later in the tutorial.

First setup the example

import numpy as np
import matplotlib.pyplot as plt

from pyapprox.benchmarks import setup_benchmark

np.random.seed(1)
shifts = [.1, .2]
benchmark = setup_benchmark(
    "tunable_model_ensemble", theta1=np.pi/2*.95, shifts=shifts)

Now define a function that computes MC estimates of the mean using different sample sets \(\rvset_N\) and plots the distribution the MC estimator \(Q_{\alpha}(\rvset_N)\), computed from 1000 different sets, and the exact value of the mean \(Q_{\alpha}\)

def plot_estimator_histrogram(nsamples, model_id, ax):
    ntrials = 1000
    np.random.seed(1)
    means = np.empty((ntrials))
    model = benchmark.funs[model_id]
    for ii in range(ntrials):
        samples = benchmark.variable.rvs(nsamples)
        values = model(samples)
        means[ii] = values.mean()
    im = ax.hist(means, bins=ntrials//100, density=True, alpha=0.3,
                 label=r'$Q_{%d}(\mathcal{Z}_{%d})$' % (model_id, nsamples))[2]
    ax.axvline(x=benchmark.fun.get_means()[model_id], alpha=1,
               label=r'$Q_{%d}$' % model_id, c=im[0].get_facecolor())

Now lets plot the historgram of the MC estimator \(Q_{0}(\rvset_N)\) using \(N=100\) samples

nsamples = int(1e2)
model_id = 0
ax = plt.subplots(1, 1, figsize=(8, 6))[1]
plot_estimator_histrogram(nsamples, model_id, ax)
_ = ax.legend()

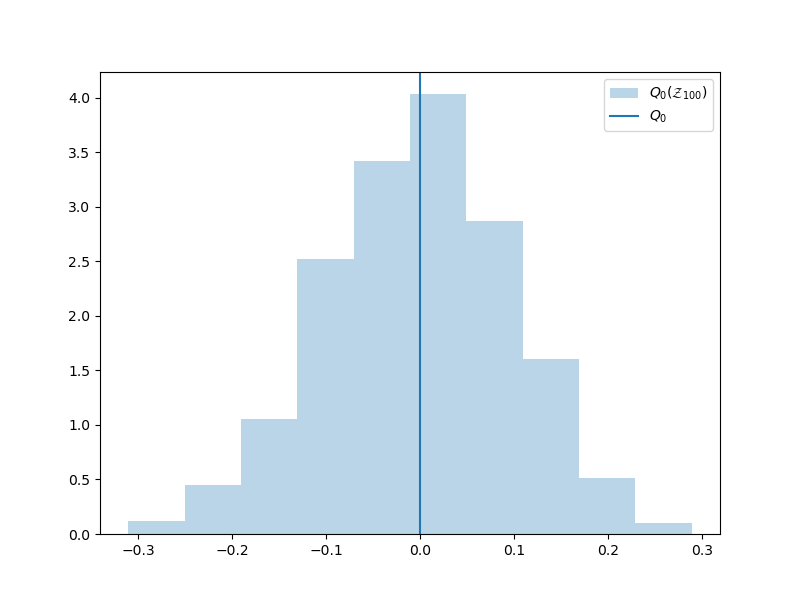
The variability of the MC estimator as we change \(\rvset_N\) decreases as we increase \(N\). To see this, plot the estimator historgram using \(N=1000\) samples

model_id = 0
ax = plt.subplots(1, 1, figsize=(8, 6))[1]
nsamples = int(1e2)
plot_estimator_histrogram(nsamples, model_id, ax)
nsamples = int(1e3)
plot_estimator_histrogram(nsamples, model_id, ax)
_ = ax.legend()

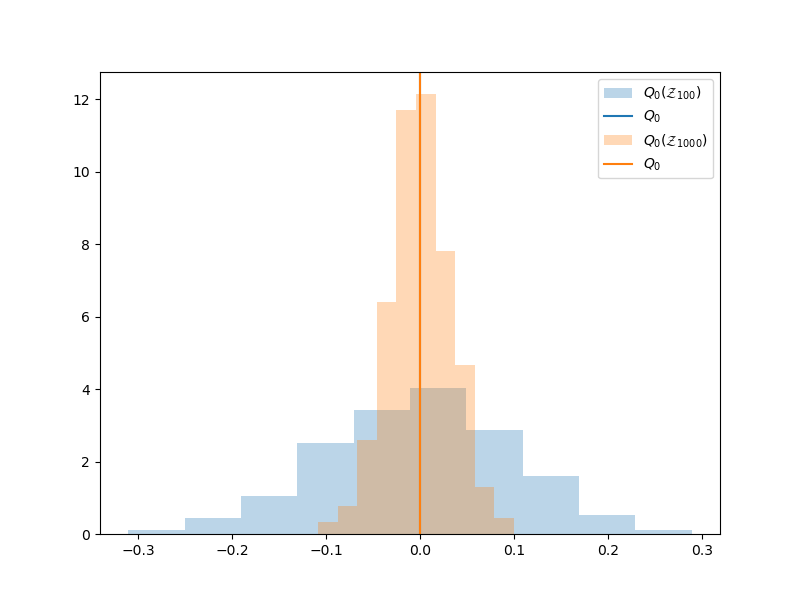
Regardless of the value of \(N\) the estimator \(Q_{0}(\rvset_N)\) is an unbiased estimate of \(Q_{0}\), that is

\[\mean{Q_{0}(\rvset_N)}-Q_0 = 0\]

Unfortunately, if the computational cost of evaluating a model is high, then one may not be able to make \(N\) large using that model. Consequently, one will not be able to trust the MC estimate of the mean much because any one realization of the estimator, computed using a single sample set, may obtain a value that is very far from the truth. So often a cheaper less accurate model is used so that \(N\) can be increased to reduce the variability of the estimator. The following compares the histograms of \(Q_0(\rvset_{100})\) and \(Q_1(\rvset_{1000})\) which uses the model \(f_1\) which we assume is a cheap approximation of \(f_0\)

model_id = 0
ax = plt.subplots(1, 1, figsize=(8, 6))[1]
nsamples = int(1e2)
plot_estimator_histrogram(nsamples, model_id, ax)
model_id = 1
nsamples = int(1e3)
plot_estimator_histrogram(nsamples, model_id, ax)
_ = ax.legend()

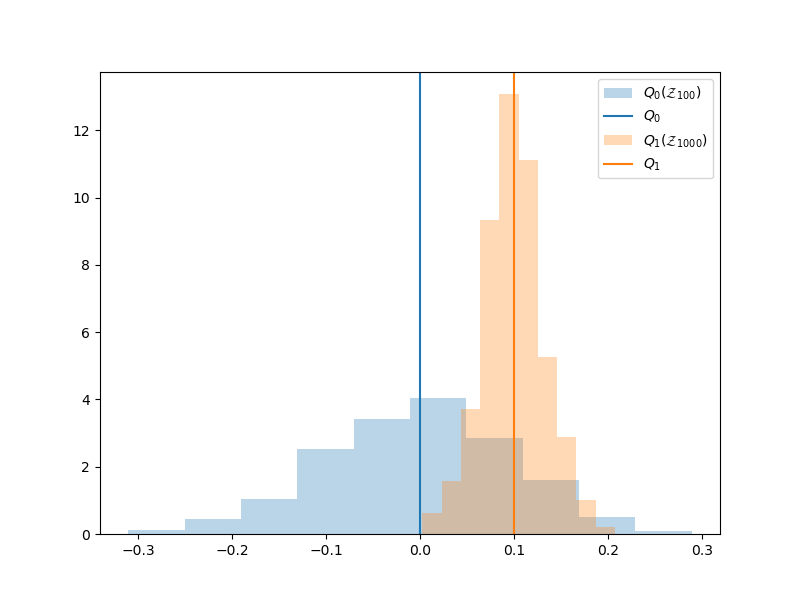
However, using an approximate model means that the MC estimator is no longer unbiased. The mean of the histogram of \(Q_1(\rvset_{1000})\) is no longer the mean of \(Q_0\)

Letting \(Q\) denote the true mean we want to estimate, e.g. \(Q=Q_0\) in the example we have used so far, the mean squared error (MSE) is typically used to quantify the quality of a MC estimator. The MSE can be expressed as

\[\begin{split}\mean{\left(Q_{\alpha}(\rvset_N)-Q\right)^2}&=\mean{\left(Q_{\alpha}(\rvset_N)-\mean{Q_{\alpha}(\rvset_N)}+\mean{Q_{\alpha}(\rvset_N)}-Q\right)^2}\\ &=\mean{\left(Q_{\alpha}(\rvset_N)-\mean{Q_{\alpha}(\rvset_N)}\right)^2}+\mean{\left(\mean{Q_{\alpha}(\rvset_N)}-Q\right)^2}\\ &\qquad\qquad+\mean{2\left(Q_{\alpha}(\rvset_N)-\mean{Q_{\alpha}(\rvset_N)}\right)\left(\mean{Q_{\alpha}(\rvset_N)}-Q\right)}\\ &=\var{Q_{\alpha}(\rvset_N)}+\left(\mean{Q_{\alpha}(\rvset_N)}-Q\right)^2\\ &=\var{Q_{\alpha}(\rvset_N)}+\left(Q_{\alpha}-Q\right)^2\end{split}\]

where the expectation \(\mathbb{E}\) and variance \(\mathbb{V}\) are taken over different realization of the sample set \(\rvset_N\), we used that \(\mean{\left(Q_{\alpha}(\rvset_N)-\mean{Q_{\alpha}(\rvset_N)}\right)}=0\) so the third term on the second line is zero, and we used \(\mean{Q_{\alpha}(\rvset_N)}=Q_{\alpha}\) to get the final equality.

Now using the well known result that for random variable \(X_n\)

\[\var{\sum_{n=1}^N X_n} = \sum_{n=1}^N \var{X_n} + \sum_{n\neq p}\covar{X_n}{X_p}\]

and the result for a scalar \(a\)

\[\var{aX_n} =a^2\var{X_n}\]

yields

\[\var{Q_{\alpha}(\rvset_N)}=\var{N^{-1}\sum_{n=1}^N f^{(n)}_\alpha}=N^{-2}\sum_{n=1}^N \var{f^{(n)}_\alpha}=N^{-1}\var{f_\alpha}\]

where \(\covar{f^{(n)}}{f^{(p)}}=0, n\neq p\) because the samples are drawn independently.

Finally, substituting \(\var{Q_{\alpha}(\rvset_N)}\) into the expression for MSE yields

\[\mean{\left(Q_{\alpha}(\rvset_N)-\mean{Q}\right)^2}=\underbrace{N^{-1}\var{f_\alpha}}_{I}+\underbrace{\left(Q_{\alpha}-Q\right)^2}_{II}\]

From this expression we can see that the MSE can be decomposed into two terms; a so called stochastic error (I) and a deterministic bias (II). The first term is the variance of the Monte Carlo estimator which comes from using a finite number of samples. The second term is due to using an approximation of \(f_0\). These two errors should be balanced, however in the vast majority of all MC analyses a single model \(f_\alpha\) is used and the choice of \(\alpha\), e.g. mesh resolution, is made a priori without much concern for the balancing bias and variance.

Video

Click on the image below to view a video tutorial on Monte Carlo quadrature