Show the Proof

import proveit
# Automation is not needed when only showing a stored proof:
proveit.defaults.automation = False # This will speed things up.
proveit.defaults.inline_pngs = False # Makes files smaller.
%show_proof

	step type	requirements	statement
0	instantiation	1, 2, 3	, , ,  ⊢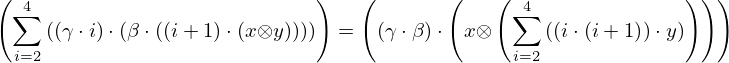
	: , : , :
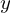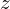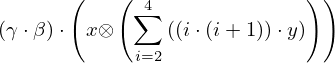1	reference	72	⊢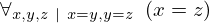
2	instantiation	55, 4, 5*, 6*	, , ,  ⊢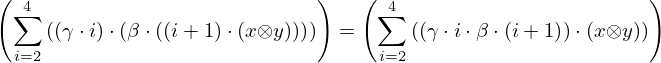
	: , : , :
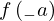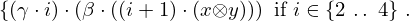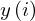3	instantiation	72, 7, 8	, , ,  ⊢
	: , : , :
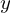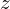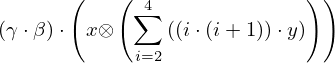4	modus ponens	9, 10	, , ,  ⊢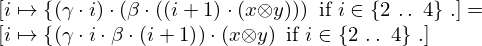
5	instantiation	79, 139	⊢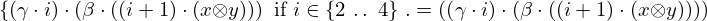
	: , :
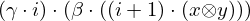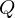6	instantiation	79, 139	⊢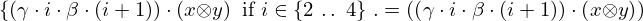
	: , :
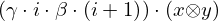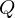7	instantiation	72, 11, 12	, , ,  ⊢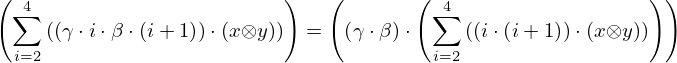
	: , : , :
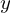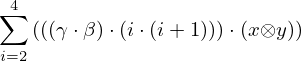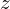8	instantiation	55, 13	,  ⊢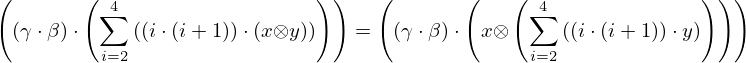
	: , : , :
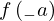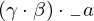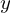9	instantiation	94, 95	⊢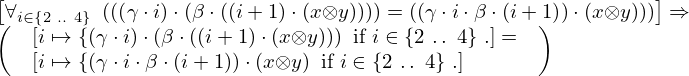
	: , : , : , : , : , : , :
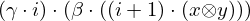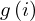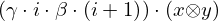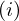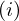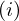10	generalization	14	, , ,  ⊢
11	instantiation	72, 15, 16	,  ⊢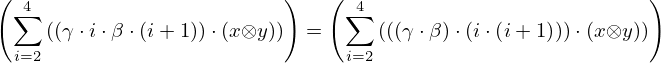
	: , : , :
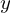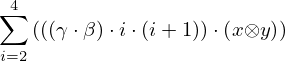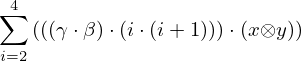12	instantiation	18, 17	, , ,  ⊢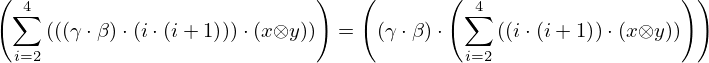
	: , :
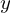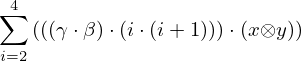13	instantiation	18, 19	,  ⊢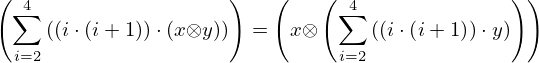
	: , :
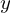14	instantiation	72, 20, 21	, , , ,  ⊢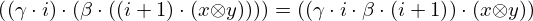
	: , : , :
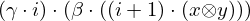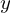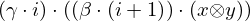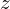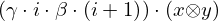15	instantiation	72, 22, 23	,  ⊢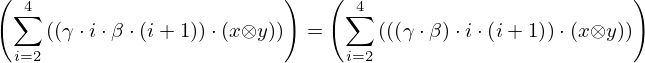
	: , : , :
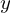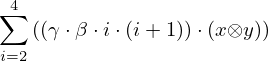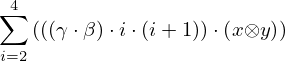16	instantiation	55, 24, 39*, 25*	,  ⊢
	: , : , :
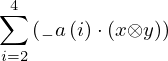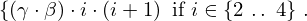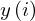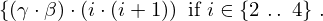17	modus ponens	26, 27	, , ,  ⊢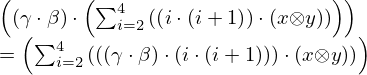
18	theorem		⊢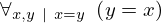
	proveit.logic.equality.equals_reversal
19	modus ponens	28, 29	,  ⊢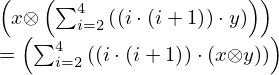
20	instantiation	30, 144, 31, 32, 33, 34	, , , ,  ⊢
	: , : , : , :
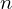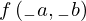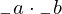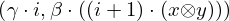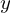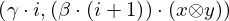21	instantiation	47, 48, 49, 51, 90, 35*	, , , ,  ⊢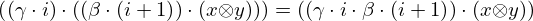
	: , : , : , : , :
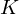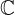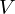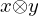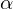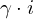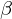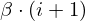22	instantiation	72, 36, 37	,  ⊢
	: , : , :
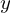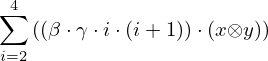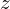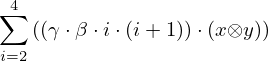23	instantiation	55, 38, 58*, 39*	,  ⊢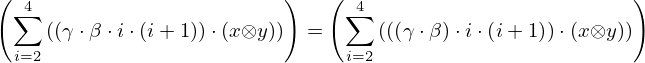
	: , : , :
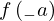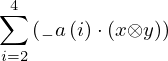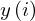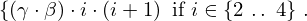24	modus ponens	40, 41	,  ⊢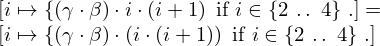
25	instantiation	79, 139	⊢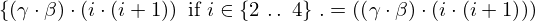
	: , :
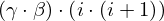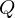26	instantiation	42, 95, 83, 99	,  ⊢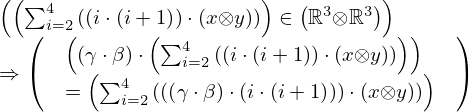
	: , : , : , : , : , : , : , :
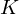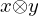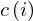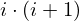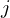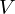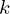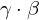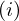27	modus ponens	43, 44	,  ⊢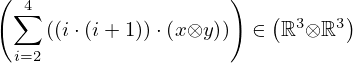
28	instantiation	45, 140, 95, 113, 83, 114	⊢
	: , : , : , : , : , : , : , : , : , : , :
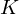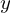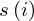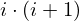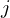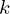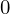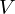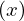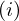29	generalization	46	,  ⊢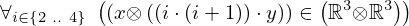
30	axiom		⊢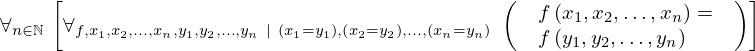
	proveit.core_expr_types.operations.operands_substitution
31	instantiation	124	⊢
	: , :
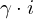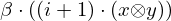32	instantiation	124	⊢
	: , :
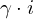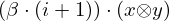33	instantiation	70, 117, 118	,  ⊢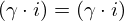
	: , :
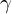34	instantiation	47, 48, 49, 116, 119, 50*	, , ,  ⊢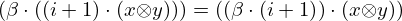
	: , : , : , : , :
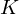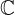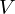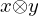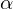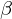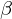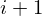35	instantiation	70, 51, 90, 52*	, ,  ⊢
	: , :
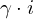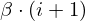36	instantiation	55, 53, 54*, 57*	,  ⊢
	: , : , :
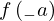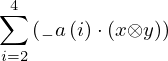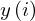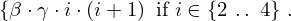37	instantiation	55, 56, 57*, 58*	,  ⊢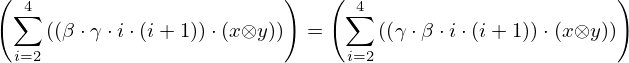
	: , : , :
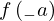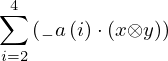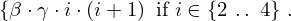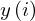38	modus ponens	59, 60	,  ⊢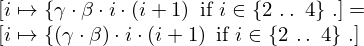
39	instantiation	79, 139	⊢
	: , :
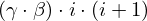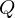40	instantiation	94, 95	⊢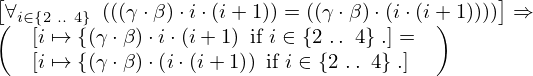
	: , : , : , : , : , : , :
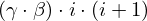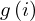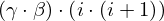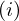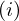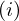41	generalization	61	,  ⊢
42	theorem		⊢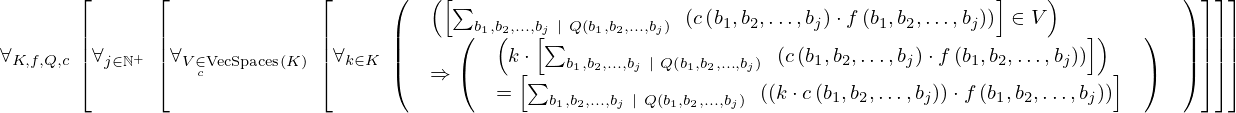
	proveit.linear_algebra.scalar_multiplication.distribution_over_vec_sum_with_scalar_mult
43	instantiation	62, 95, 83	⊢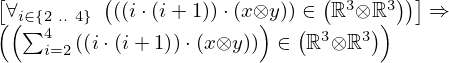
	: , : , : , : , : , :
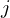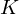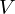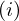44	generalization	64	,  ⊢
45	theorem		⊢
	proveit.linear_algebra.tensors.tensor_prod_distribution_over_summation_with_scalar_mult
46	instantiation	63, 64, 65	, ,  ⊢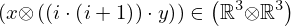
	: , : , :
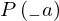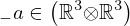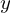47	theorem		⊢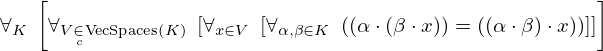
	proveit.linear_algebra.scalar_multiplication.doubly_scaled_as_singly_scaled
48	instantiation	100, 102, 66, 67	⊢
	: , : , :
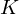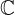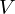49	instantiation	101, 102, 66, 67, 105, 68, 69	,  ⊢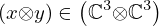
	: , : , : , :
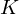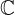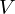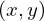50	instantiation	70, 116, 119	,  ⊢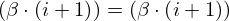
	: , :
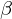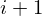51	instantiation	145, 127, 71	,  ⊢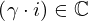
	: , : , :
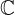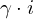52	instantiation	72, 73, 74	, ,  ⊢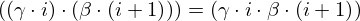
	: , : , :
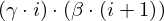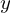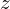53	modus ponens	75, 76	,  ⊢
54	instantiation	79, 139	⊢
	: , :
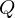55	axiom		⊢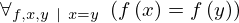
	proveit.logic.equality.substitution
56	modus ponens	77, 78	,  ⊢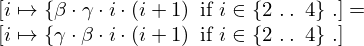
57	instantiation	79, 139	⊢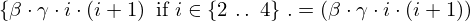
	: , :
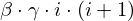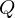58	instantiation	79, 139	⊢
	: , :
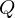59	instantiation	94, 95	⊢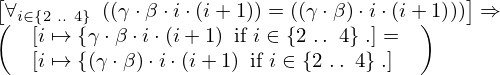
	: , : , : , : , : , : , :
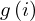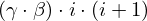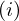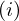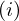60	generalization	80	,  ⊢
61	instantiation	97, 140, 144, 113, 115, 114, 81, 118, 119	, ,  ⊢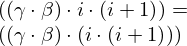
	: , : , : , : , : , :
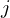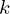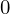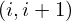62	theorem		⊢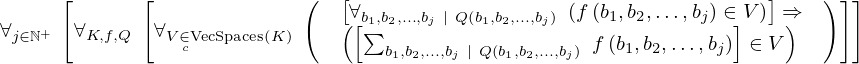
	proveit.linear_algebra.addition.summation_closure
63	theorem		⊢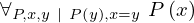
	proveit.logic.equality.sub_left_side_into
64	instantiation	82, 83, 86, 84	, ,  ⊢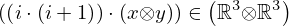
	: , : , : , :
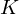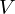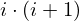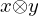65	instantiation	85, 86, 140, 113, 114, 104, 106, 107	, ,  ⊢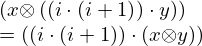
	: , : , : , : , : , : , : , : , : , :
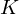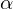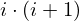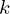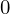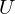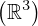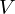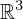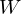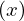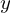66	instantiation	124	⊢
	: , :
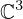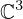67	instantiation	87, 122	⊢
	:
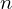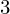68	instantiation	88, 89, 106	⊢
	: , : , :
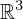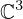69	instantiation	88, 89, 107	⊢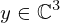
	: , : , :
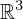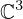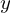70	axiom		⊢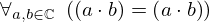
	proveit.linear_algebra.scalar_multiplication.scalar_mult_extends_number_mult
71	instantiation	120, 126, 130	,  ⊢
	: , :
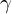72	axiom		⊢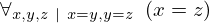
	proveit.logic.equality.equals_transitivity
73	instantiation	91, 113, 144, 140, 114, 111, 117, 118, 90	, ,  ⊢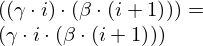
	: , : , : , : , : , :
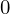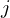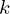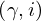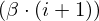74	instantiation	91, 144, 113, 111, 92, 114, 117, 118, 116, 119	, ,  ⊢
	: , : , : , : , : , :
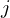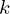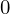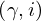75	instantiation	94, 95	⊢
	: , : , : , : , : , : , :
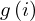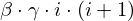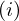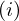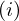76	generalization	93	,  ⊢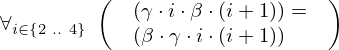
77	instantiation	94, 95	⊢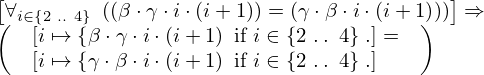
	: , : , : , : , : , : , :
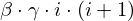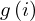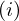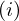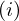78	generalization	96	,  ⊢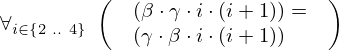
79	theorem		⊢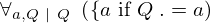
	proveit.core_expr_types.conditionals.satisfied_condition_reduction
80	instantiation	97, 113, 144, 114, 98, 115, 117, 116, 118, 119	, ,  ⊢
	: , : , : , : , : , :
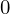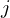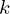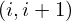81	instantiation	145, 127, 99	,  ⊢
	: , : , :
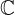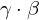82	theorem		⊢
	proveit.linear_algebra.scalar_multiplication.scalar_mult_closure
83	instantiation	100, 102, 103, 104	⊢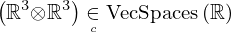
	: , : , :
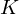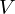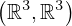84	instantiation	101, 102, 103, 104, 105, 106, 107	,  ⊢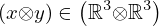
	: , : , : , :
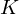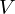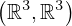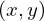85	theorem		⊢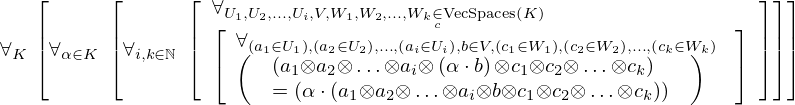
	proveit.linear_algebra.tensors.factor_scalar_from_tensor_prod
86	instantiation	120, 130, 128	⊢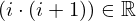
	: , :
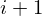87	theorem		⊢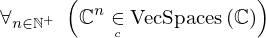
	proveit.linear_algebra.complex_vec_set_is_vec_space
88	theorem		⊢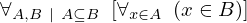
	proveit.logic.sets.inclusion.unfold_subset_eq
89	instantiation	108, 122, 109	⊢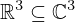
	: , : , :
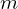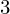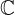90	instantiation	110, 116, 119	,  ⊢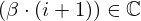
	: , :
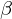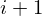91	theorem		⊢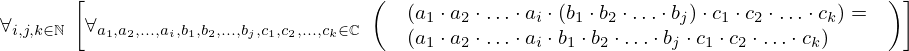
	proveit.numbers.multiplication.disassociation
92	instantiation	124	⊢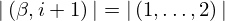
	: , :
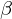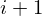93	instantiation	112, 113, 144, 140, 114, 111, 117, 118, 116, 119	, ,  ⊢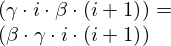
	: , : , : , : , : , : , :
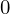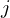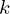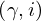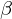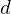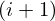94	theorem		⊢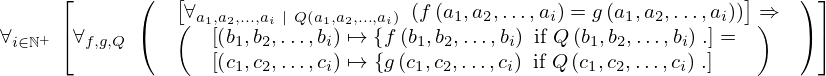
	proveit.core_expr_types.lambda_maps.general_lambda_substitution
95	theorem		⊢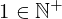
	proveit.numbers.numerals.decimals.posnat1
96	instantiation	112, 113, 140, 144, 114, 115, 116, 117, 118, 119	, ,  ⊢
	: , : , : , : , : , : , :
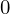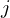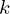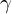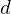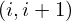97	theorem		⊢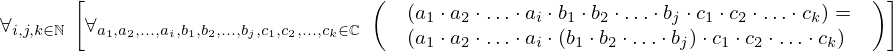
	proveit.numbers.multiplication.association
98	instantiation	124	⊢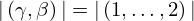
	: , :
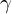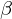99	instantiation	120, 126, 125	,  ⊢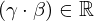
	: , :
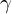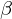100	theorem		⊢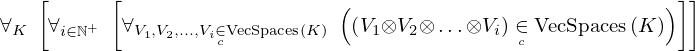
	proveit.linear_algebra.tensors.tensor_prod_of_vec_spaces_is_vec_space
101	theorem		⊢
	proveit.linear_algebra.tensors.tensor_prod_is_in_tensor_prod_space
102	theorem		⊢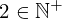
	proveit.numbers.numerals.decimals.posnat2
103	instantiation	124	⊢
	: , :
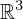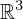104	instantiation	121, 122	⊢
	:
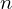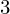105	instantiation	124	⊢
	: , :
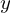106	assumption		⊢
107	assumption		⊢
108	theorem		⊢
	proveit.logic.sets.cartesian_products.cart_exp_subset_eq
109	instantiation	123, 127	⊢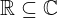
	: , :
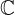110	theorem		⊢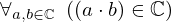
	proveit.numbers.multiplication.mult_complex_closure_bin
111	instantiation	124	⊢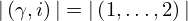
	: , :
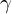112	theorem		⊢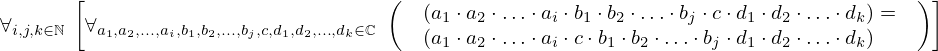
	proveit.numbers.multiplication.leftward_commutation
113	axiom		⊢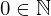
	proveit.numbers.number_sets.natural_numbers.zero_in_nats
114	theorem		⊢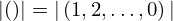
	proveit.core_expr_types.tuples.tuple_len_0_typical_eq
115	instantiation	124	⊢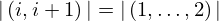
	: , :
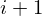116	instantiation	145, 127, 125	⊢
	: , : , :
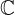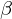117	instantiation	145, 127, 126	⊢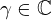
	: , : , :
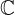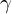118	instantiation	145, 127, 130	⊢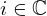
	: , : , :
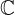119	instantiation	145, 127, 128	⊢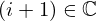
	: , : , :
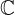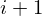120	theorem		⊢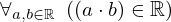
	proveit.numbers.multiplication.mult_real_closure_bin
121	theorem		⊢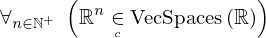
	proveit.linear_algebra.real_vec_set_is_vec_space
122	theorem		⊢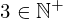
	proveit.numbers.numerals.decimals.posnat3
123	theorem		⊢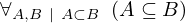
	proveit.logic.sets.inclusion.relax_proper_subset
124	theorem		⊢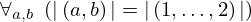
	proveit.numbers.numerals.decimals.tuple_len_2_typical_eq
125	assumption		⊢
126	assumption		⊢
127	theorem		⊢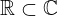
	proveit.numbers.number_sets.complex_numbers.real_within_complex
128	instantiation	129, 130, 131	⊢
	: , :
129	theorem		⊢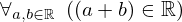
	proveit.numbers.addition.add_real_closure_bin
130	instantiation	145, 133, 132	⊢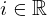
	: , : , :
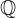131	instantiation	145, 133, 134	⊢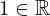
	: , : , :
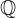132	instantiation	145, 136, 135	⊢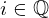
	: , : , :
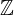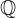133	theorem		⊢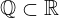
	proveit.numbers.number_sets.real_numbers.rational_within_real
134	instantiation	145, 136, 137	⊢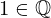
	: , : , :
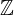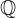135	instantiation	145, 138, 139	⊢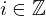
	: , : , :
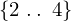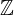136	theorem		⊢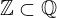
	proveit.numbers.number_sets.rational_numbers.int_within_rational
137	instantiation	145, 146, 140	⊢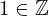
	: , : , :
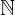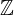138	instantiation	141, 142, 143	⊢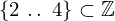
	: , :
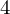139	assumption		⊢
140	theorem		⊢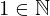
	proveit.numbers.numerals.decimals.nat1
141	theorem		⊢
	proveit.numbers.number_sets.integers.int_interval_within_int
142	instantiation	145, 146, 144	⊢
	: , : , :
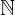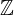143	instantiation	145, 146, 147	⊢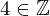
	: , : , :
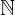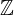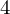144	theorem		⊢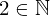
	proveit.numbers.numerals.decimals.nat2
145	theorem		⊢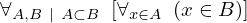
	proveit.logic.sets.inclusion.superset_membership_from_proper_subset
146	theorem		⊢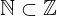
	proveit.numbers.number_sets.integers.nat_within_int
147	theorem		⊢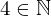
	proveit.numbers.numerals.decimals.nat4
*equality replacement requirements