Note

Click here to download the full example code

Surrogate Modeling

Many simulation models are extremely computationally expensive such that adequately understanding their behaviour and quantifying uncertainty can be computationally intractable for any of the aforementioned techniques. Various methods have been developed to produce surrogates of the model response to uncertain parameters, the most efficient are goal-oriented in nature and target very specific uncertainty measures.

Generally speaking surrogates are built using a ``small’’ number of model simulations and are then substituted in place of the expensive simulation models in future analysis. Some of the most popular surrogate types include polynomial chaos expansions (PCE) [XKSISC2002], Gaussian processes (GP) [RWMIT2006], and sparse grids (SG) [BGAN2004].

Reduced order models (e.g. [SFIJNME2017]) can also be used to construct surrogates and have been applied successfully for UQ on many applications. These methods do not construct response surface approximations, but rather solve the governing equations on a reduced basis. PyApprox does not currently implement reduced order modeling, however the modeling analyis tools found in PyApprox can easily be applied to assess or design systems based on reduced order models.

The use of surrogates for model analysis consists of two phases: (1) construction; and (2) post-processing.

Construction

In this section we show how to construct a surrogate using tensor-product Lagrange interpolation.

Tensor-product Lagrange interpolation

Let \(\hat{f}_{\boldsymbol{\alpha},\boldsymbol{\beta}}(\mathbf{z})\) be an M-point tensor-product interpolant of the function \(\hat{f}_{\boldsymbol{\alpha}}\). This interpolant is a weighted linear combination of tensor-product of univariate Lagrange polynomials

\[\phi_{i,j}(z_i) = \prod_{k=1,k\neq j}^{m_{\beta_i}}\frac{z_i-z_i^{(k)}}{z_i^{(j)}-z_i^{(k)}}, \quad i\in[d],\]

defined on a set of univariate points \(z_{i}^{(j)},j\in[m_{\beta_i}]\) Specifically the multivariate interpolant is given by

\[\hat{f}_{\boldsymbol{\alpha},\boldsymbol{\beta}}(\mathbf{z}) = \sum_{\boldsymbol{j}\le\boldsymbol{\beta}} \hat{f}_{\boldsymbol{\alpha}}(\mathbf{z}^{(\boldsymbol{j})})\prod_{i\in[d]}\phi_{i,j_i}(z_i).\]

The partial ordering \(\boldsymbol{j}\le\boldsymbol{\beta}\) is true if all the component wise conditions are true.

Constructing the interpolant requires evaluating the function \(\hat{f}_{\boldsymbol{\alpha}}\) on the grid of points

\[\mathcal{Z}_{\boldsymbol{\beta}} = \bigotimes_{i=1}^d \mathcal{Z}_{\beta_i}^i=\begin{bmatrix}\mathbf{z}^{(1)} & \cdots&\mathbf{z}^{(M_{\boldsymbol{\beta}})}\end{bmatrix}\in\mathbb{R}^{d\times M_{\boldsymbol{\beta}}}\]

We denote the resulting function evaluations by

\[\mathcal{F}_{\boldsymbol{\alpha},\boldsymbol{\beta}}=\hat{f}_{\boldsymbol{\alpha}}(\mathcal{Z}_{\boldsymbol{\beta}})=\begin{bmatrix}\hat{f}_{\boldsymbol{\alpha}}(\mathbf{z}^{(1)}) \quad \cdots\quad \hat{f}_{\boldsymbol{\alpha}}(\mathbf{z}^{(M_{\boldsymbol{\beta}})})\end{bmatrix}^T\in\mathbb{R}^{M_{\boldsymbol{\beta}}\times q},\]

where the number of points in the grid is \(M_{\boldsymbol{\beta}}=\prod_{i\in[d]} m_{\beta_i}\)

It is often reasonable to assume that, for any \(\mathbf{z}\), the cost of each simulation is constant for a given \(\boldsymbol{\alpha}\). So letting \(W_{\boldsymbol{\alpha}}\) denote the cost of a single simulation, we can write the total cost of evaluating the interpolant \(W_{\boldsymbol{\alpha},\boldsymbol{\beta}}=W_{\boldsymbol{\alpha}} M_{\boldsymbol{\beta}}\). Here we have assumed that the computational effort to compute the interpolant once data has been obtained is negligible, which is true for sufficiently expensive models \(\hat{f}_{\boldsymbol{\alpha}}\). Here we will use the nested Clenshaw-Curtis points

\[z_{i}^{(j)}=\cos\left(\frac{(j-1)\pi}{m_{\beta_i}}\right),\qquad j=1,\ldots,m_{\beta_i}\]

to define the univariate Lagrange polynomials. The number of points \(m(l)\) of this rule grows exponentially with the level \(l\), specifically \(m(0)=1\) and \(m(l)=2^{l}+1\) for \(l\geq1\). The univariate Clenshaw-Curtis points, the tensor-product grid \(\mathcal{Z}_{\boldsymbol{\beta}}\), and two multivariate Lagrange polynomials with their corresponding univariate Lagrange polynomials are shown below for \(\boldsymbol{\beta}=(2,2)\).

from pyapprox.examples.tensor_product_lagrange_interpolation import *
fig = plt.figure(figsize=(2*8,6))
ax=fig.add_subplot(1,2,1,projection='3d')
level = 2; ii=1; jj=1
plot_tensor_product_lagrange_basis_2d(level,ii,jj,ax)

ax=fig.add_subplot(1,2,2,projection='3d')
level = 2; ii=1; jj=3
plot_tensor_product_lagrange_basis_2d(level,ii,jj,ax)
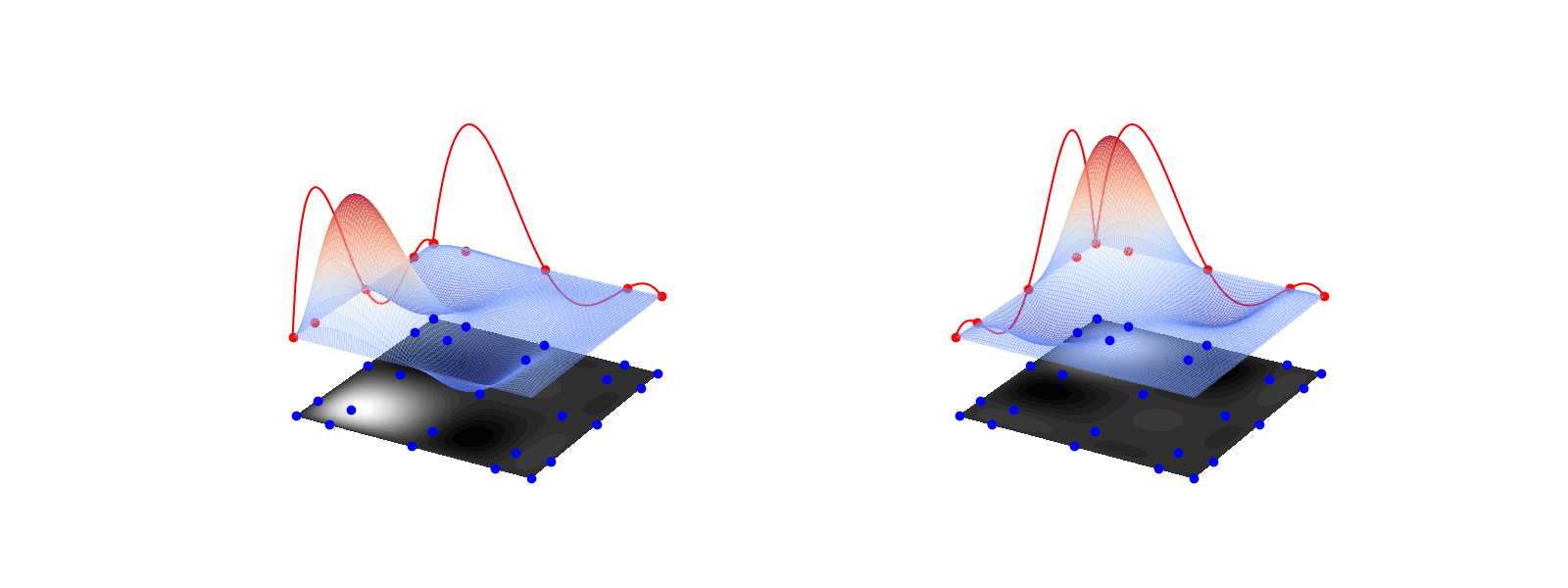
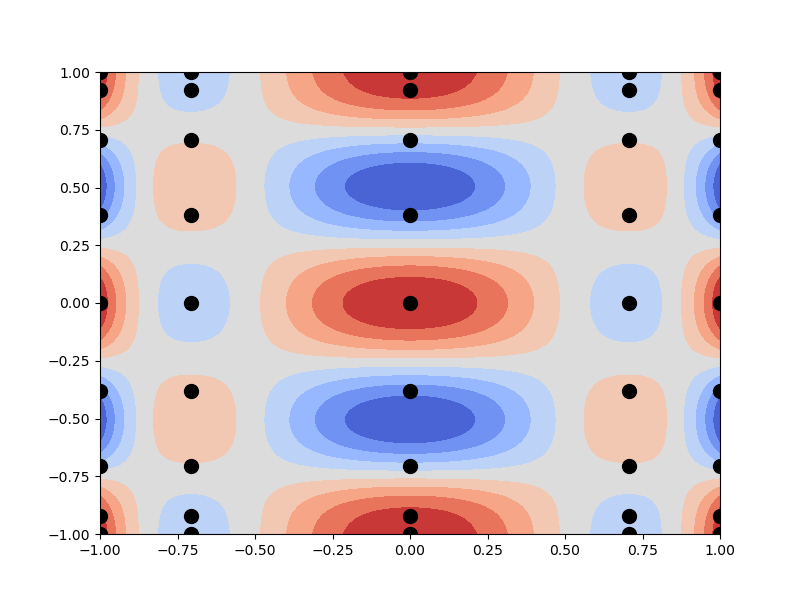
plot tensor product interpolation

To construct a surrogate using tensor product interpolation we simply multiply all such basis functions by the value of the function \(f_\ai\) evaluated at the corresponding interpolation point. The following uses tensor product interpolation to approximate the simple function

\[f_\ai(\rv) = \cos(2\pi\rv_1)\cos(2\pi\rv_2), \qquad \rv\in\rvdom=[-1,1]^2\]
f = lambda z : (np.cos(2*np.pi*z[0,:])*np.cos(2*np.pi*z[1,:]))[:,np.newaxis]
def get_interpolant(function,level):
    level = np.asarray(level)
    univariate_samples_func = lambda l: pya.clenshaw_curtis_pts_wts_1D(l)[0]
    abscissa_1d = [univariate_samples_func(level[0]),
                   univariate_samples_func(level[1])]


    samples_1d = pya.get_1d_samples_weights(
        [pya.clenshaw_curtis_in_polynomial_order]*2,
        [pya.clenshaw_curtis_rule_growth]*2,level)[0]

    poly_indices = pya.get_subspace_polynomial_indices(
        level,[pya.clenshaw_curtis_rule_growth]*2,config_variables_idx=None)
    samples = pya.get_subspace_samples(level,poly_indices,samples_1d)
    fn_vals = function(samples)

    interp = lambda samples: pya.evaluate_sparse_grid_subspace(
        samples,level,fn_vals,samples_1d,None,False)
    hier_indices = pya.get_hierarchical_sample_indices(
        level,poly_indices,samples_1d,config_variables_idx=None)

    return interp, samples, hier_indices, abscissa_1d[0].shape[0], \
      abscissa_1d[1].shape[0]

import pyapprox as pya
level = [2,3]
interp,samples,_ = get_interpolant(f,level)[:3]

marker_color='k'
alpha=1.0
fig,axs = plt.subplots(1,1,figsize=(8,6))
axs.plot(samples[0,:],samples[1,:],'o',color=marker_color,ms=10,alpha=alpha)

plot_limits = [-1,1,-1,1]
num_pts_1d = 101
X,Y,Z = get_meshgrid_function_data(
    interp, plot_limits, num_pts_1d)

num_contour_levels=10
import matplotlib as mpl
cmap = mpl.cm.coolwarm
levels = np.linspace(Z.min(),Z.max(),num_contour_levels)
cset = axs.contourf(
    X, Y, Z, levels=levels,cmap=cmap,alpha=alpha)
plt.show()
plot tensor product interpolation

The error in the tensor product interpolant is given by

\[\lVert f_\ai-f_{\ai,\bi}\rVert_{L^\infty(\rvdom)} \le C_{d,r} N_{\bi}^{-s/d}\]

Post-processing

Once a surrogate has been constructed it can be used for many different purposes. For example one can use it to estimate moments, perform sensitivity analysis, or simply approximate the evaluation of the expensive model at new locations where expensive simulation model data is not available.

To use the surrogate for computing moments we simply draw realizations of the input random variables \(\rv\) and evaluate the surrogate at those samples. We can approximate the mean of the expensive simluation model as the average of the surrogate values at the random samples.

We know from Monte Carlo Quadrature that the error in the Monte carlo estimate of the mean using the surrogate is

\[\begin{split}\mean{\left(Q_{\alpha}-\mean{Q}\right)^2}&=N^{-1}\var{Q_\alpha}+\left(\mean{Q_{\alpha}}-\mean{Q}\right)^2\\ &\le N^{-1}\var{Q_\alpha}+C_{d,r} N_{\bi}^{-s/d}\end{split}\]

Because a surrogate is inexpensive to evaluate the first term can be driven to zero so that only the bias remains. Thus the error in the Monte Carlo estimate of the mean using the surrogate is dominated by the error in the surrogate. If this error can be reduced more quickly than frac{N^{-1}} (as is the case for low-dimensional tensor-product interpolation) then using surrogates for computing moments is very effective.

Note that moments can be estimated without using Monte-Carlo sampling by levaraging properties of the univariate interpolation rules used to build the multi-variate interpolant. Specifically, the expectation of a tensor product interpolant can be computed without explicitly forming the interpolant and is given by

\[\mu_{\bi}=\int_{\rvdom} \sum_{\V{j}\le\bi}f_\ai(\rv^{(\V{j})})\prod_{i=1}^d\phi_{i,j_i}(\rv_i) w(\rv)\,d\rv=\sum_{\V{j}\le\bi} f_\ai(\rv^{(\V{j})}) v_{\V{j}}.\]

The expectation is simply the weighted sum of the Cartesian-product of the univariate quadrature weights

\[v_{\V{j}}=\prod_{i=1}^d\int_{\rvdom_i}{\phi_{i,j_i}(\rv_i)}\,dw(\rv_i),\]

which can be computed analytically.

x,w=pya.get_tensor_product_quadrature_rule(
    level,2,pya.clenshaw_curtis_pts_wts_1D)
surrogate_mean = f(x)[:,0].dot(w)
print('Quadrature mean',surrogate_mean)

Out:

Quadrature mean 0.00010032278321495927

Here we have recomptued the values of \(f\) at the interpolation samples, but in practice we sould just re-use the values collected when building the interpolant.

Now let us compare the quadrature mean with the MC mean computed using the surrogate

num_samples = int(1e6)
samples = np.random.uniform(-1,1,(2,num_samples))
values = interp(samples)
mc_mean = values.mean()
print('Monte Carlo surrogate mean',mc_mean)

Out:

Monte Carlo surrogate mean 2.4970335218097065e-05