Theory & Practice

Note

This theory section is intended to give a very high-level understanding of key concepts for WecOptTool. For a more detailed explanation, please see [1, 2, 3].

Basic concept

WecOptTool uses a pseudo-spectral method [4] to perform two tasks simultaneously:

1. Optimize the solution for the desired objective function (e.g. power generation)

2. Simulate the wave energy converter (WEC) dynamics

This can be written as a traditional optimization problem:

(1)$$\begin{array}{r}\underset{x}{min}J(x)\\ \text{s.t.}& \\ r(x)& =0\\ c_{ineq}(x)& \le 0\\ c_{eq}(x)& =0\end{array}$$

Here, $x$ is the state vector which includes both the WEC dynamic state ($x_w$) and the user-defined control state to be optimized ($x_u$), as $x=[x_w,x_u]$. We wish to find optimal values for $x_u$ to minimize the objective function $J(x)$. This accomplishes task 1 from above. The solution is forced to follow the dynamics of the system via the constraint $r(x)=0$, where $r(x)$ is the WEC dynamics equation in residual form. This accomplishes task 2 from above. The dynamic residual includes the linear hydrodynamic forces from a BEM solution plus any number of arbitrary nonlinear forces such as power take-off (PTO) force, mooring forces, and non-linear hydrodynamic forces. Additionally, any number of arbitrary nonlinear constraints, such as requiring a tether to remain in tension or limiting the maximum force exerted by the PTO, can be included in $c_{ineq}(x)$ and $c_{eq}(x)$.

Solving (1), we can find the optimal control state $x_u$ (e.g., PTO force) that minimizes our objective function (e.g., power generation) for a given WEC design subject to arbitrary constraints and including nonlinear dynamics. The pseudo-spectral method has a number of key attributes that make it well-suited to this application:

• Explicit constraints: Dynamic and kinematic constraints can be enforced explicitly, negating the need to run unfeasible solutions and thus reducing computational cost.

• Efficient simulation of nonlinear dynamics: Frequency-domain solutions cannot include nonlinear dynamics and time-domain solutions can only do so with significant computational cost; the pseudo-spectral method can efficiently handle nonlinear systems.

• Arbitrary or fixed controller structure: As a starting point, one may consider optimal control without a given structure. Later on, it may be useful to consider, e.g., a proportional feedback or latching controller. This can be accomplished via the pseudo-spectral method by structuring the system dynamics and the control vector ($x_u$).

The solution to (1) can be wrapped with an outer design optimization problem, in which any optimization algorithm can be applied. Some examples of problems which can be addressed within this framework include:

• Optimization of geometry dimensions for a hull

• Optimization of PTO components (e.g., inertia of a flywheel, a gear ratio)

• Optimization of ballast versus pre-tension

• Optimization of the layout for a WEC array

How’s this different from what I’m used to?

Most users will be more familiar with a time-stepping approach for differential equations–this is the method applied in Simulink and therefore WEC-Sim. Starting from an initial time (e.g., $t=0$), the solution is solved by iteratively stepping forward in time.

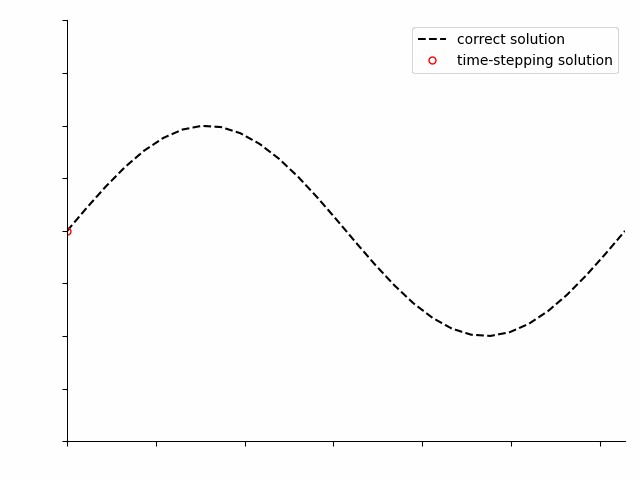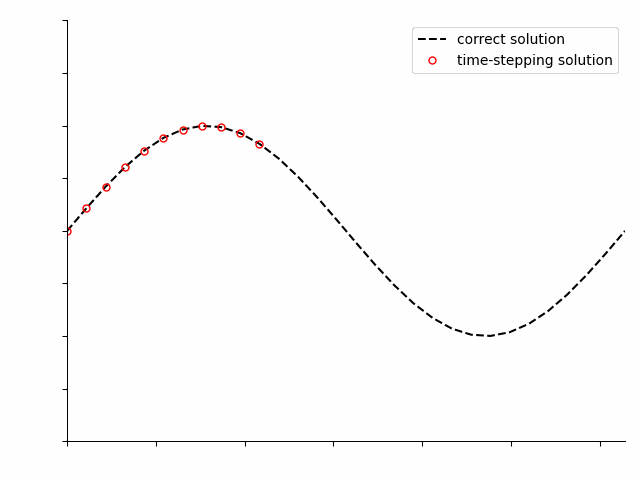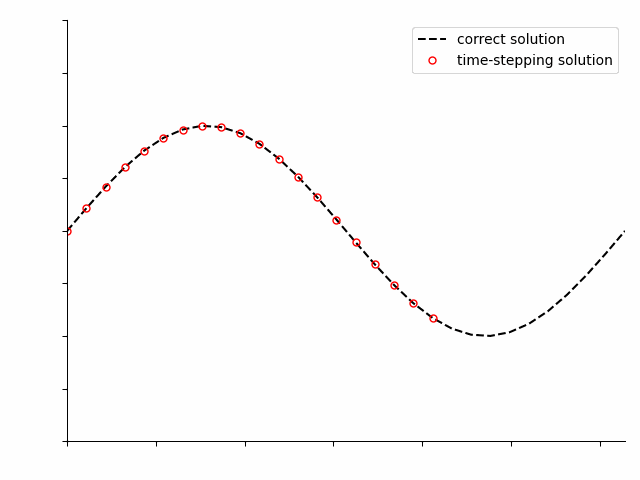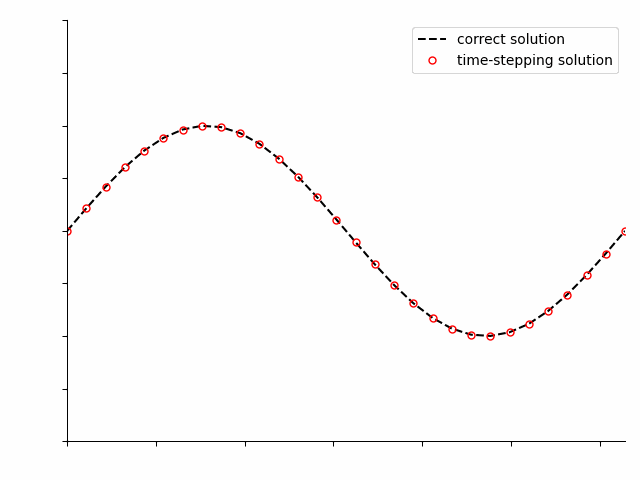
Pseudo-spectral methods can be applied to solve the same differential equations, but solve the entire time period of interest at once. At first the solution will not be correct, but as the optimization algorithm iterates, it will progressively improve the solution.

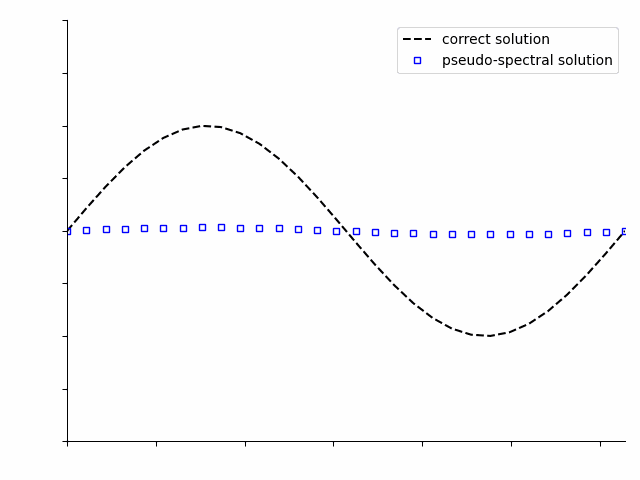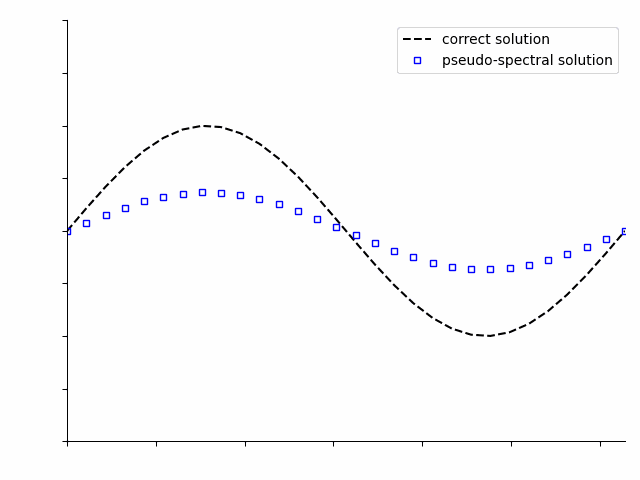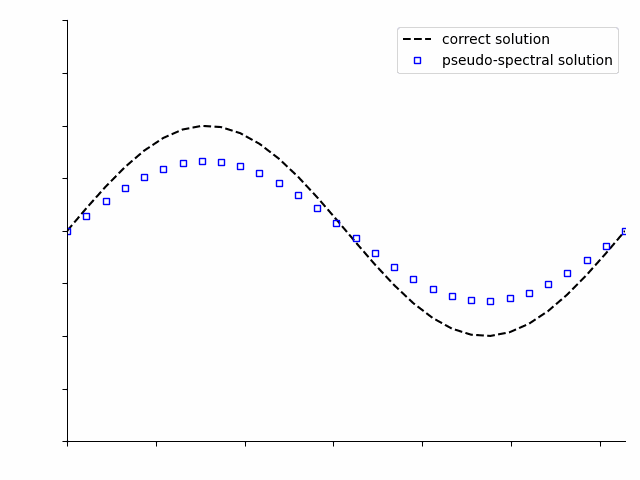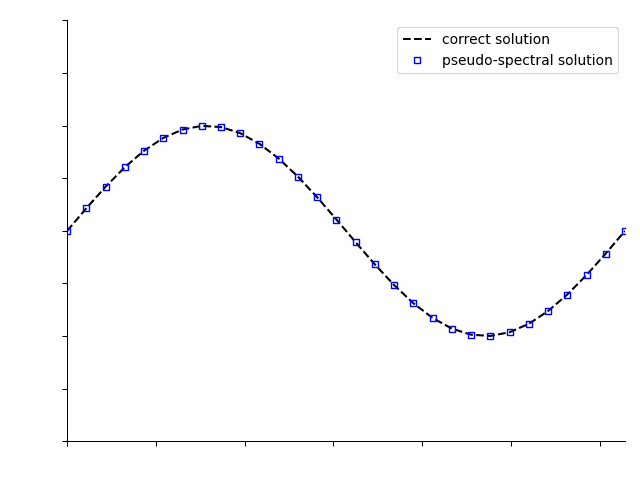
Note

These animations are simplifications and do not fully capture all details of either the time-stepping or pseudo-spectral numerical optimization solution.

Practical concerns

Frequencies

The solution to (1) will be found by projecting the time-domain trajectories into the frequency domain (see further discussion in Implementation). To control this process, the user must specify an equally spaced frequency array (see wecopttool.frequency()). When creating this frequency array, consider:

• Exciting frequencies of the wave and, if you expect a nonlinear response, superharmonics of the exciting frequencies

• Power absorption occurs at two times the exciting frequencies (only important for visualization)

• The fundamental frequency is also the frequency step ($f_1=\mathrm{\Delta }f$); set this sufficiently small to resolve the wave spectra and frequency response functions of interest

Automatic differentiation

In practice, the size of the decision vector $x$ from (1) will often be quite large. For a single degree of freedom device, $x$ can easily be $\mathcal{O}(1e2)$. To obtain high accuracy solutions to optimization problems with large numbers of decision variables, without requiring users to provide analytic gradients (i.e., the Jacobian and Hessian matrices), WecOptTool employs the automatic differentiation package Autograd. In practice, most WecOptTool users should only need to know that when writing custom functions to define their device, they should simply use the Autograd replacement for NumPy by calling import autograd.numpy as np. Note that Autograd does not support all of NumPy (see the Autograd documentation) and using unsupported parts can result in silent failure of the automatic differentiation.

Scaling

For many WEC problems, (1) will be poorly scaled. Recall that $x=[x_w,x_u]$, where $x_w$ describes the state of the WEC (e.g., velocities) and $x_u$ is a vector to be optimized to maximize power absorption. Consider, for example, a general case without a controller structure, in which $x_u$ would relate to PTO forces. For a wave tank scale device, one might expect velocities of $\mathcal{O}(1e-1)$, but the forces could be $\mathcal{O}(1e3)$. For larger WECs, this discrepancy in the orders of magnitude may be even worse. Scaling mismatches in the decision variable $x$ and with the objective function $J(x)$ can lead to problems with convergence.

Constraints

Constraints, such as maximum PTO force, maximum piston force, or maintaining tension in a tether, may be enforced in WecOptTool. This functionality is well-illustrated in Tutorial 1 - WaveBot. An important practical factor when using this functionality is to make sure that the constraint is evaluated at a sufficient number of collocation points. It may be required to enforce constraints at more points than the dynamics (as defined by the frequency array). In WecOptTool’s example PTO module, this is controlled by the nsubsteps argument (see, e.g., wecopttool.pto.PTO.force_on_wec()).

Buoyancy/gravity

As WecOptTool is intended primarily to utilize linear potential flow hydrodynamics, a linear hydrostatic stiffness is used. The implicit assumption of this approach is that the body is neutrally buoyant (i.e., gravitational and buoyancy forces are in balance at the zero position). However, some WECs achieve equilibrium through a pretension applied via mooring and/or the PTO. In this case, the device can still be modeled with the linear hydrostatic stiffness, but if you wish to solve for the pretension force in your simulations, you may explicitly include the buoyancy, gravity, and pretension forces via the f_add argument to wecopttool.core.WEC.

PTO Kinematics

The wecopttool.pto module includes several examples of PTOs that can be used for both additional PTO forces on the WEC dynamics and for objective functions (e.g., PTO average power). Creating one of these pre-defined PTOs requires specifying the kinematics matrix. Here, the kinematics matrix, $K$, is defined as the linear transformation from the WEC position (e.g., heave) in the global frame, $x$, to the PTO position in the PTO frame (e.g., tether length/generator rotation), $p$:

(2)$$p=Kx$$

The relationship $p(x)$ is typically referred to as the backward kinematics, in the field of robotics. If the WEC were considered to be a robot it’s hydrodynamic body would be equivalent to an end effector represented in a global coordinate frame. The PTO positions would be equivalent to joint positions in local coordinates. The matrix $K$ has a size equal to the number of DOFs of the PTOs times the number of DOFs of the WEC. Note, however that the real kinematics might not be linear. Equation (2) represents a linearization of $p(x)$ about the mean $x=0$ position, with the matrix $K$ being the inverse Jacobian of $p(x)$ at $x=0$.

The transpose of $K$ is used to transform the PTO forces in PTO frame, $f_p$, to the PTO forces on the WEC, $f_w$:

(3)$$f_w=K^T{f}_p$$

This relationship can be derived from conservation of energy in both frames, and using the definition in (2):

(4)$$\begin{array}{r}{f}_w^{T}x=f_p^{T}p\\ f_w^{T}x=f_p^{T}Kx\\ f_w^T=f_p^{T}K\\ f_w=K^T{f}_p\end{array}$$

Phase Realizations

Irregular waves are defined in WecOptTool as a spectrum of complex frequency-domain wave elevations. The phase of each of the elevation elements impacts the time-domain result. Thus, the standard calculation of the objective function (average power) may change across a range of phase realizations. The amount of variance in power depends on multiple factors such as the optimization problem and the frequency array. When creating an irregular wave using wecopttool.waves.long_crested_wave() or wecopttool.waves.irregular_wave(), nrealizations can be used to select the number of phase realizations to be used. By default, random realizations will be used to create the selected number of wave elevation spectra. The wecopttool.WEC.solve() function will automatically iterate through and solve the optimization problem for each realization, and the overall result can be found by averaging the value of the objective function across all realizations. A general recommendation is to use sufficient random phase realizations such that the total simulation time sums to 20 minutes.

(5)$$t_{total}=\frac{nrealizations}{f1}$$

The selection of the number of realizations is further detailed in Tutorial 4 - Pioneer.

Troubleshooting

If your simulation is not behaving as expected, consider some of the general troubleshooting steps below:

• Check that the hydrodynamic coefficients are displaying expected behavior for high frequencies:

  • Added mass asymptotes to finite value

  • Radiation damping asymptotes to zero

• Check for irregular frequencies in the hydrodynamics. If necessary, alter the mesh and frequencies to avoid/remove these

• Check that the hydrostatic stiffness and mass properties match your hand calculations

• Check that absorbed power is less than or equal to the theoretical maximum