logo

Expression of type ExprTuple

from the theory of proveit.physics.quantum.circuits

In [1]:
import proveit
# Automation is not needed when building an expression:
proveit.defaults.automation = False # This will speed things up.
proveit.defaults.inline_pngs = False # Makes files smaller.
%load_expr # Load the stored expression as 'stored_expr'
# import Expression classes needed to build the expression
from proveit import ExprTuple
from proveit.physics.quantum.circuits import QcircuitEquiv, circuit_Akm, circuit_Bkn, circuit_permuted_Akm, circuit_permuted_Bkn
In [2]:
# build up the expression from sub-expressions
expr = ExprTuple(QcircuitEquiv(circuit_Akm, circuit_Bkn), QcircuitEquiv(circuit_permuted_Akm, circuit_permuted_Bkn))
expr:
In [3]:
# check that the built expression is the same as the stored expression
assert expr == stored_expr
assert expr._style_id == stored_expr._style_id
print("Passed sanity check: expr matches stored_expr")

Passed sanity check: expr matches stored_expr
In [4]:
# Show the LaTeX representation of the expression for convenience if you need it.
print(stored_expr.latex())

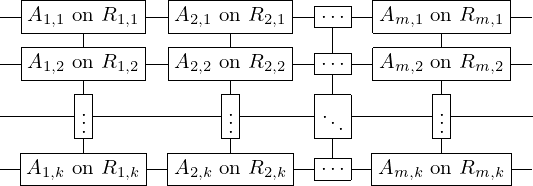
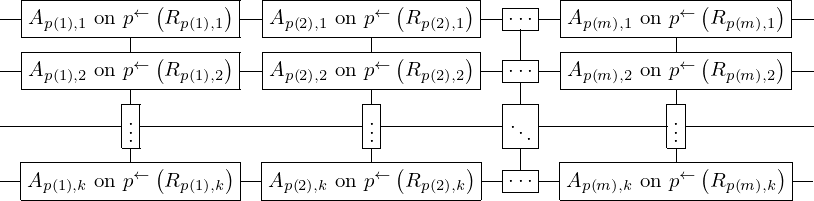
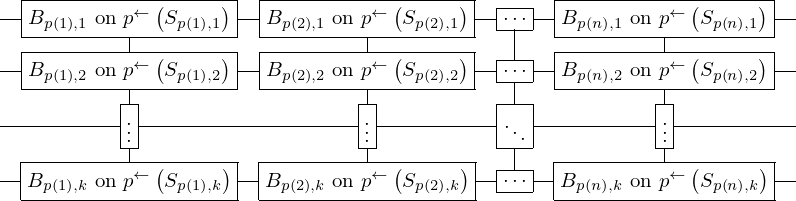
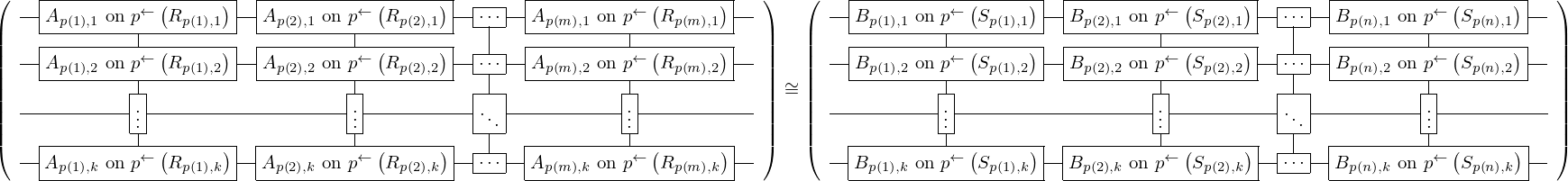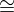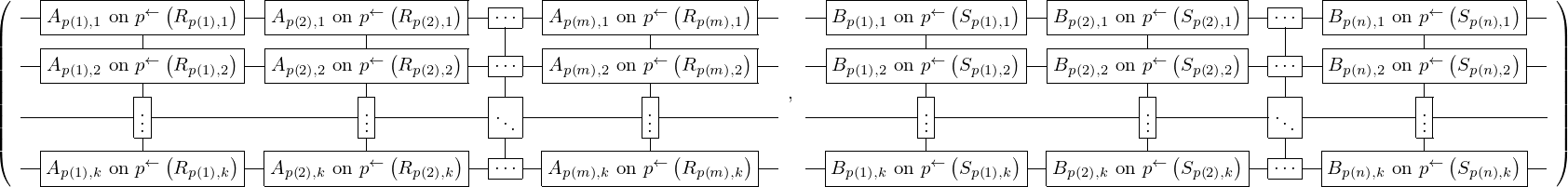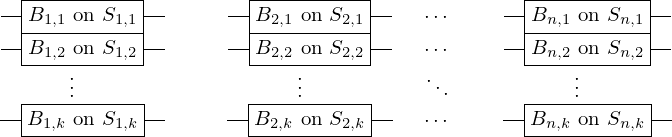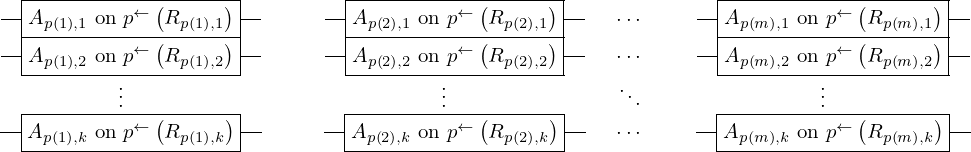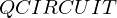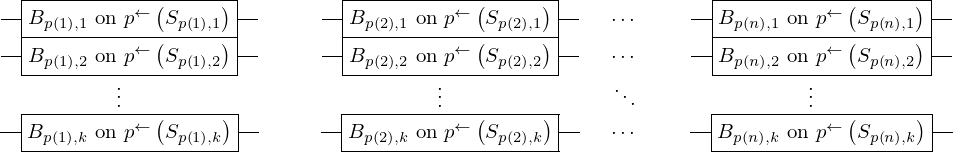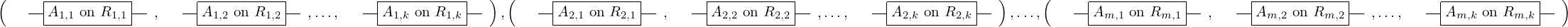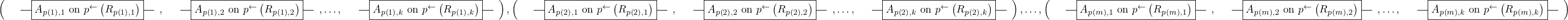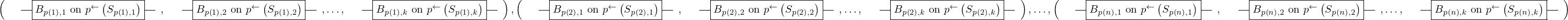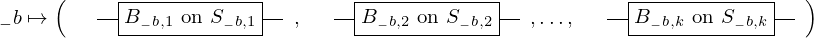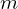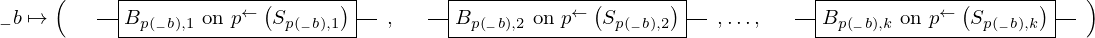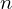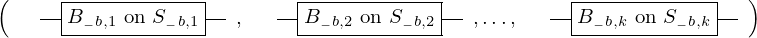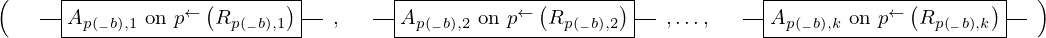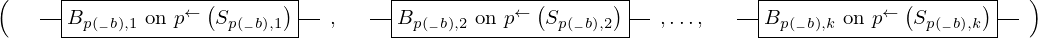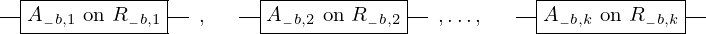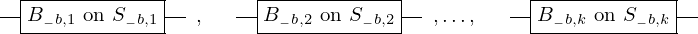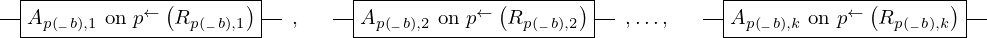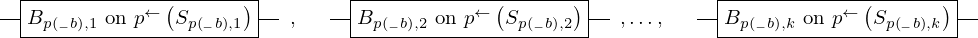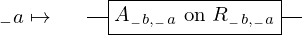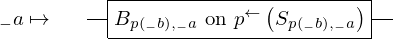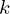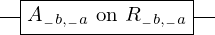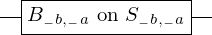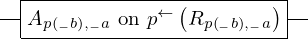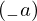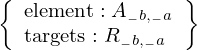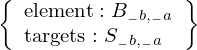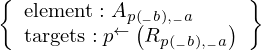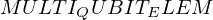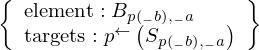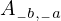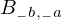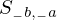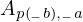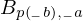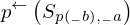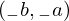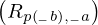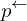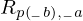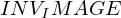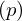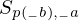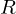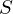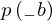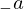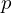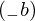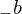\left(\left(\begin{array}{c} \Qcircuit@C=1em @R=.7em{
& \gate{A_{1, 1}~\mbox{on}~R_{1, 1}} \qwx[1] & \gate{A_{2, 1}~\mbox{on}~R_{2, 1}} \qwx[1] & \gate{\cdots} \qwx[1] & \gate{A_{m, 1}~\mbox{on}~R_{m, 1}} \qwx[1] & \qw \\
& \gate{A_{1, 2}~\mbox{on}~R_{1, 2}} \qwx[1] & \gate{A_{2, 2}~\mbox{on}~R_{2, 2}} \qwx[1] & \gate{\cdots} \qwx[1] & \gate{A_{m, 2}~\mbox{on}~R_{m, 2}} \qwx[1] & \qw \\
& \gate{\vdots} \qwx[1] & \gate{\vdots} \qwx[1] & \gate{\ddots} \qwx[1] & \gate{\vdots} \qwx[1] & \qw \\
& \gate{A_{1, k}~\mbox{on}~R_{1, k}} & \gate{A_{2, k}~\mbox{on}~R_{2, k}} & \gate{\cdots} & \gate{A_{m, k}~\mbox{on}~R_{m, k}} & \qw
} \end{array}\right) \cong \left(\begin{array}{c} \Qcircuit@C=1em @R=.7em{
& \gate{B_{1, 1}~\mbox{on}~S_{1, 1}} \qwx[1] & \gate{B_{2, 1}~\mbox{on}~S_{2, 1}} \qwx[1] & \gate{\cdots} \qwx[1] & \gate{B_{n, 1}~\mbox{on}~S_{n, 1}} \qwx[1] & \qw \\
& \gate{B_{1, 2}~\mbox{on}~S_{1, 2}} \qwx[1] & \gate{B_{2, 2}~\mbox{on}~S_{2, 2}} \qwx[1] & \gate{\cdots} \qwx[1] & \gate{B_{n, 2}~\mbox{on}~S_{n, 2}} \qwx[1] & \qw \\
& \gate{\vdots} \qwx[1] & \gate{\vdots} \qwx[1] & \gate{\ddots} \qwx[1] & \gate{\vdots} \qwx[1] & \qw \\
& \gate{B_{1, k}~\mbox{on}~S_{1, k}} & \gate{B_{2, k}~\mbox{on}~S_{2, k}} & \gate{\cdots} & \gate{B_{n, k}~\mbox{on}~S_{n, k}} & \qw
} \end{array}\right), \left(\begin{array}{c} \Qcircuit@C=1em @R=.7em{
& \gate{A_{p\left(1\right), 1}~\mbox{on}~p^{\leftarrow}\left(R_{p\left(1\right), 1}\right)} \qwx[1] & \gate{A_{p\left(2\right), 1}~\mbox{on}~p^{\leftarrow}\left(R_{p\left(2\right), 1}\right)} \qwx[1] & \gate{\cdots} \qwx[1] & \gate{A_{p\left(m\right), 1}~\mbox{on}~p^{\leftarrow}\left(R_{p\left(m\right), 1}\right)} \qwx[1] & \qw \\
& \gate{A_{p\left(1\right), 2}~\mbox{on}~p^{\leftarrow}\left(R_{p\left(1\right), 2}\right)} \qwx[1] & \gate{A_{p\left(2\right), 2}~\mbox{on}~p^{\leftarrow}\left(R_{p\left(2\right), 2}\right)} \qwx[1] & \gate{\cdots} \qwx[1] & \gate{A_{p\left(m\right), 2}~\mbox{on}~p^{\leftarrow}\left(R_{p\left(m\right), 2}\right)} \qwx[1] & \qw \\
& \gate{\vdots} \qwx[1] & \gate{\vdots} \qwx[1] & \gate{\ddots} \qwx[1] & \gate{\vdots} \qwx[1] & \qw \\
& \gate{A_{p\left(1\right), k}~\mbox{on}~p^{\leftarrow}\left(R_{p\left(1\right), k}\right)} & \gate{A_{p\left(2\right), k}~\mbox{on}~p^{\leftarrow}\left(R_{p\left(2\right), k}\right)} & \gate{\cdots} & \gate{A_{p\left(m\right), k}~\mbox{on}~p^{\leftarrow}\left(R_{p\left(m\right), k}\right)} & \qw
} \end{array}\right) \cong \left(\begin{array}{c} \Qcircuit@C=1em @R=.7em{
& \gate{B_{p\left(1\right), 1}~\mbox{on}~p^{\leftarrow}\left(S_{p\left(1\right), 1}\right)} \qwx[1] & \gate{B_{p\left(2\right), 1}~\mbox{on}~p^{\leftarrow}\left(S_{p\left(2\right), 1}\right)} \qwx[1] & \gate{\cdots} \qwx[1] & \gate{B_{p\left(n\right), 1}~\mbox{on}~p^{\leftarrow}\left(S_{p\left(n\right), 1}\right)} \qwx[1] & \qw \\
& \gate{B_{p\left(1\right), 2}~\mbox{on}~p^{\leftarrow}\left(S_{p\left(1\right), 2}\right)} \qwx[1] & \gate{B_{p\left(2\right), 2}~\mbox{on}~p^{\leftarrow}\left(S_{p\left(2\right), 2}\right)} \qwx[1] & \gate{\cdots} \qwx[1] & \gate{B_{p\left(n\right), 2}~\mbox{on}~p^{\leftarrow}\left(S_{p\left(n\right), 2}\right)} \qwx[1] & \qw \\
& \gate{\vdots} \qwx[1] & \gate{\vdots} \qwx[1] & \gate{\ddots} \qwx[1] & \gate{\vdots} \qwx[1] & \qw \\
& \gate{B_{p\left(1\right), k}~\mbox{on}~p^{\leftarrow}\left(S_{p\left(1\right), k}\right)} & \gate{B_{p\left(2\right), k}~\mbox{on}~p^{\leftarrow}\left(S_{p\left(2\right), k}\right)} & \gate{\cdots} & \gate{B_{p\left(n\right), k}~\mbox{on}~p^{\leftarrow}\left(S_{p\left(n\right), k}\right)} & \qw
} \end{array}\right)\right)
In [5]:
stored_expr.style_options()
namedescriptiondefaultcurrent valuerelated methods
wrap_positionsposition(s) at which wrapping is to occur; 'n' is after the nth comma.()()('with_wrapping_at',)
justificationif any wrap positions are set, justify to the 'left', 'center', or 'right'leftleft('with_justification',)
In [6]:
# display the expression information
stored_expr.expr_info()
 core typesub-expressionsexpression
0ExprTuple1, 2
1Operationoperator: 4
operands: 3
2Operationoperator: 4
operands: 5
3ExprTuple6, 7
4Literal
5ExprTuple8, 9
6Operationoperator: 13
operands: 10
7Operationoperator: 13
operands: 11
8Operationoperator: 13
operands: 12
9Operationoperator: 13
operands: 14
10ExprTuple15
11ExprTuple16
12ExprTuple17
13Literal
14ExprTuple18
15ExprRangelambda_map: 19
start_index: 37
end_index: 22
16ExprRangelambda_map: 20
start_index: 37
end_index: 24
17ExprRangelambda_map: 21
start_index: 37
end_index: 22
18ExprRangelambda_map: 23
start_index: 37
end_index: 24
19Lambdaparameter: 74
body: 25
20Lambdaparameter: 74
body: 26
21Lambdaparameter: 74
body: 27
22Variable
23Lambdaparameter: 74
body: 28
24Variable
25ExprTuple29
26ExprTuple30
27ExprTuple31
28ExprTuple32
29ExprRangelambda_map: 33
start_index: 37
end_index: 38
30ExprRangelambda_map: 34
start_index: 37
end_index: 38
31ExprRangelambda_map: 35
start_index: 37
end_index: 38
32ExprRangelambda_map: 36
start_index: 37
end_index: 38
33Lambdaparameter: 71
body: 39
34Lambdaparameter: 71
body: 40
35Lambdaparameter: 71
body: 41
36Lambdaparameter: 71
body: 43
37Literal
38Variable
39Operationoperator: 47
operands: 44
40Operationoperator: 47
operands: 45
41Operationoperator: 47
operands: 46
42ExprTuple71
43Operationoperator: 47
operands: 48
44NamedExprselement: 49
targets: 50
45NamedExprselement: 51
targets: 52
46NamedExprselement: 53
targets: 54
47Literal
48NamedExprselement: 55
targets: 56
49IndexedVarvariable: 58
indices: 57
50IndexedVarvariable: 67
indices: 57
51IndexedVarvariable: 60
indices: 57
52IndexedVarvariable: 68
indices: 57
53IndexedVarvariable: 58
indices: 69
54Operationoperator: 61
operand: 63
55IndexedVarvariable: 60
indices: 69
56Operationoperator: 61
operand: 66
57ExprTuple74, 71
58Variable
59ExprTuple63
60Variable
61Operationoperator: 64
operand: 72
62ExprTuple66
63IndexedVarvariable: 67
indices: 69
64Literal
65ExprTuple72
66IndexedVarvariable: 68
indices: 69
67Variable
68Variable
69ExprTuple70, 71
70Operationoperator: 72
operand: 74
71Variable
72Variable
73ExprTuple74
74Variable