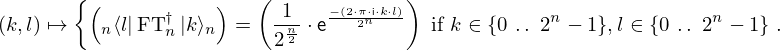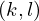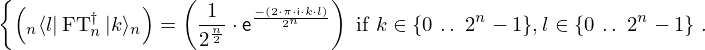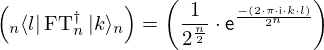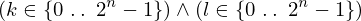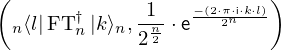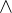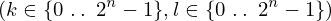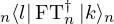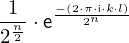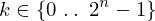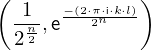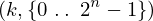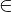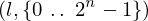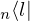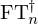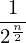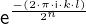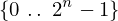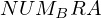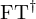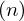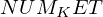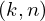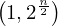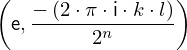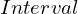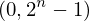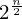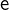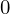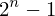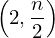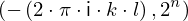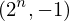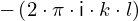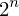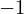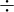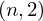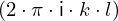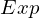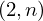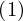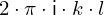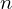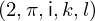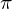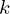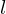Expression of type Lambda

from the theory of proveit.physics.quantum.QFT

import proveit
# Automation is not needed when building an expression:
proveit.defaults.automation = False # This will speed things up.
proveit.defaults.inline_pngs = False # Makes files smaller.
%load_expr # Load the stored expression as 'stored_expr'
# import Expression classes needed to build the expression
from proveit import Conditional, Lambda, k, l, n
from proveit.logic import And, Equals, InSet
from proveit.numbers import Exp, Interval, Mult, Neg, e, frac, i, one, pi, subtract, two, zero
from proveit.physics.quantum import NumBra, NumKet, Qmult
from proveit.physics.quantum.QFT import InverseFourierTransform

# build up the expression from sub-expressions
sub_expr1 = Exp(two, n)
sub_expr2 = Interval(zero, subtract(sub_expr1, one))
expr = Lambda([k, l], Conditional(Equals(Qmult(NumBra(l, n), InverseFourierTransform(n), NumKet(k, n)), Mult(frac(one, Exp(two, frac(n, two))), Exp(e, frac(Neg(Mult(two, pi, i, k, l)), sub_expr1)))), And(InSet(k, sub_expr2), InSet(l, sub_expr2))))

expr:

# check that the built expression is the same as the stored expression
assert expr == stored_expr
assert expr._style_id == stored_expr._style_id
print("Passed sanity check: expr matches stored_expr")

Passed sanity check: expr matches stored_expr

# Show the LaTeX representation of the expression for convenience if you need it.
print(stored_expr.latex())

\left(k, l\right) \mapsto \left\{\left({_{n}}\langle l \rvert \thinspace {\mathrm {FT}}^{\dag}_{n} \thinspace \lvert k \rangle_{n}\right) = \left(\frac{1}{2^{\frac{n}{2}}} \cdot \mathsf{e}^{\frac{-\left(2 \cdot \pi \cdot \mathsf{i} \cdot k \cdot l\right)}{2^{n}}}\right) \textrm{ if } k \in \{0~\ldotp \ldotp~2^{n} - 1\} ,  l \in \{0~\ldotp \ldotp~2^{n} - 1\}\right..

stored_expr.style_options()

no style options

# display the expression information
stored_expr.expr_info()

	core type	sub-expressions	expression
0	Lambda	parameters: 1 body: 2
1	ExprTuple	63, 64
2	Conditional	value: 3 condition: 4
3	Operation	operator: 5 operands: 6
4	Operation	operator: 7 operands: 8
5	Literal
6	ExprTuple	9, 10
7	Literal
8	ExprTuple	11, 12
9	Operation	operator: 13 operands: 14
10	Operation	operator: 58 operands: 15
11	Operation	operator: 17 operands: 16
12	Operation	operator: 17 operands: 18
13	Literal
14	ExprTuple	19, 20, 21
15	ExprTuple	22, 23
16	ExprTuple	63, 24
17	Literal
18	ExprTuple	64, 24
19	Operation	operator: 25 operands: 26
20	Operation	operator: 27 operand: 56
21	Operation	operator: 29 operands: 30
22	Operation	operator: 48 operands: 31
23	Operation	operator: 51 operands: 32
24	Operation	operator: 33 operands: 34
25	Literal
26	ExprTuple	64, 56
27	Literal
28	ExprTuple	56
29	Literal
30	ExprTuple	63, 56
31	ExprTuple	57, 35
32	ExprTuple	36, 37
33	Literal
34	ExprTuple	38, 39
35	Operation	operator: 51 operands: 40
36	Literal
37	Operation	operator: 48 operands: 41
38	Literal
39	Operation	operator: 42 operands: 43
40	ExprTuple	60, 44
41	ExprTuple	45, 46
42	Literal
43	ExprTuple	46, 47
44	Operation	operator: 48 operands: 49
45	Operation	operator: 53 operand: 55
46	Operation	operator: 51 operands: 52
47	Operation	operator: 53 operand: 57
48	Literal
49	ExprTuple	56, 60
50	ExprTuple	55
51	Literal
52	ExprTuple	60, 56
53	Literal
54	ExprTuple	57
55	Operation	operator: 58 operands: 59
56	Variable
57	Literal
58	Literal
59	ExprTuple	60, 61, 62, 63, 64
60	Literal
61	Literal
62	Literal
63	Variable
64	Variable