setup_mfnets_helmholtz_benchmark

pyapprox.fenics_models.helmholtz_benchmarks.setup_mfnets_helmholtz_benchmark(mesh_resolution=51, noise_std=1)

Setup the multi-fidelity benchmark used to combine helmholtz data.

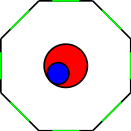
Experimental configuration. Speaker cones (green speakers), speaker cabinets (black segments), scatterer (red and blue circles).

For a fixed angular velocity \(\omega = 2\pi f\), the acoustic pressure \(u\) is modeled using the (real) Helmholtz equation defined on an open regular octagon domain \(D\) with apothem equal to 1.5 meters. The interior of \(D\) contains a scatterer (red and blue circles) and each side of the octagon consists of an individual speaker and its cabinet; the centered green boundary segments are speaker cones which comprise 0.875 of the total edge length and the black segments are the cabinet walls. To simplify the problem, we model the scatterer as a dense fluid and ignore the impedance of the speaker cabinet.

\[\Delta u + \kappa^2 u = 0 \quad\text{in }D, \qquad\qquad\frac{\partial u}{\partial n} = \rho_0\omega\sum_{j=1}^8 \theta_j\chi_j \quad\text{on }\partial D\]

where \(\kappa=\omega/c\) is the wave number, \(c\) is the speed of sound, \(\rho_0\) is the fluid density, \(\chi_j:\partial D\to\{0,1\}\) is the characteristic function of the \(j^{\text{th}}\) speaker cone (green boundary segments in the figure), and \(\theta_j\) is the acoustic velocity output by the \(j^{\text{th}}\) speaker for \(j=1,\ldots,8\) — in other words, the \(j^{\text{th}}\) speaker cone oscillates with velocity \(\theta_j\cos(\omega t)\). In this example we assume that the material in the red circle is made of aluminum for which the speed of sound is 6320 m/s and that the regions in the blue circle and exterior to the red circle are comprised of air at \(20^\circ\text{C}\) which has a speed of sound of 343 m/s. In addition, we set the frequency to be \(f=400\) Hz and the fluid density to be that of air at \(20^\circ\text{C}\) and standard atmospheric pressure, i.e. \(\rho_0=1.204 \text{kg/m}^3\).

The benchmark consists of data from three experiments each consisting of measurements of the acoustic pressure data \(u(x)\), at 5000 microphone locations \(x\). For the high-fideliy experiment we set the speaker amplitudes as \(\theta_{1,i}=1\), \(i=1,\ldots,8\) and for the low-fidelity experiments we set \(\theta_{2,i}=1\), \(i=3,5,7\) and \(\theta_{3,i}=3\), \(i=2,4,6,8\); all other speaker amplitudes are set to zero. Speakers are ordered counter clockwise with the first speaker located on the right vertical edge of the octagon.

Under these conditions each information source

\[u_1(x)=\sum_{i=1}^8 \phi_i(x)\theta_{1,i} \qquad u_2(x)=\sum_{i=3,5,7} \phi_i(x)\theta_{2,i} \qquad u_3(x)=\sum_{i=2,4,6,8} \phi_i(x)\theta_{3,i}\]

is a linear sum of basis functions \(\phi_i(x)\) which correspond to solving the Helmholtz equation using only one active speaker. Specifically the basis \(\phi_i\) is obtained by solving

\[\Delta \phi + \kappa^2 \phi = 0 \quad\text{in }D, \qquad\qquad\frac{\partial \phi}{\partial n} = \rho_0\omega\theta_i \quad\text{on }\partial D\]

The measurements of each experiment, taken at locations \(x_k^{(i)}\) in the domain \(D\), are given by \(y_k^{(i)}=u_k(x_k^{(i)})+\epsilon_k^{(i)}\) for each information source \(k=1,2,3\), where the noise \(\epsilon_k^{(i)}\) is normally distributed with mean zero and unit variance.

Parameters

mesh_resolutioninteger

Specifies the resolution of the finite element mesh

noise_stdfloat

The standard deviation of the IID noise in the observations

Returns

benchmarkpya.Benchmark

Object containing the benchmark attributes documented below

sampleslist

List with entries np.ndarray (nvars,nsamples) which contain the locations \(x_k^{(i)}\) of the observations of each information source

obslist np.ndarray (nsamples,1)

List with entries np.ndarray (nsamples,1) containing the values of the noisy observations \(y_k^{(i)}\) of each information source

basesnp.ndarray (nsamples,8)

The basis functions \(\phi_i\) used to model the observations

noise_stdfloat

The standard deviation of the IID noise in the observations. This is just the value passed in to this function, stored for convienience.