Show the Proof

import proveit
# Automation is not needed when only showing a stored proof:
proveit.defaults.automation = False # This will speed things up.
proveit.defaults.inline_pngs = False # Makes files smaller.
%show_proof

	step type	requirements	statement
0	instantiation	1, 2, 3	, , ,  ⊢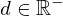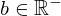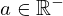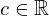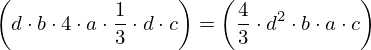
	: , : , :
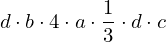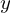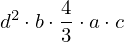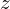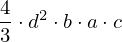1	reference	9	⊢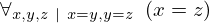
2	instantiation	4, 5, 6, 7	, , ,  ⊢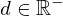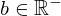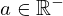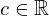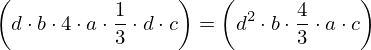
	: , : , : , :
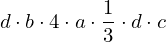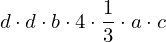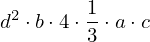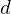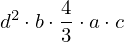3	instantiation	25, 12, 85, 14, 19, 21, 22, 27, 8, 28, 30	, , ,  ⊢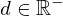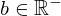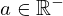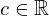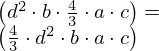
	: , : , : , : , : , : , :
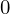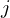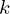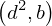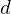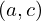4	theorem		⊢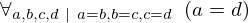
	proveit.logic.equality.four_chain_transitivity
5	instantiation	9, 10, 11	, , ,  ⊢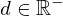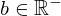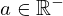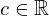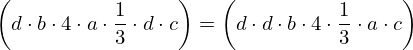
	: , : , :
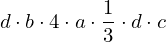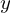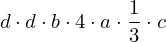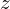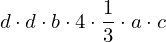6	instantiation	18, 12, 85, 13, 14, 15, 16, 52, 27, 59, 29, 28, 30, 17*	, , ,  ⊢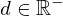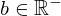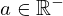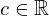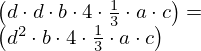
	: , : , : , : , : , :
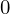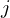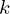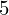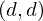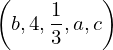7	instantiation	18, 85, 19, 20, 21, 22, 27, 59, 29, 28, 30, 23*	, , ,  ⊢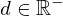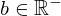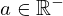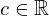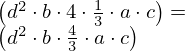
	: , : , : , : , : , :
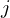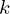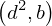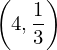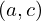8	instantiation	47, 59, 61, 49	⊢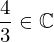
	: , :
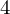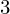9	axiom		⊢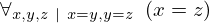
	proveit.logic.equality.equals_transitivity
10	instantiation	25, 92, 93, 24, 52, 27, 59, 28, 29, 30	, , ,  ⊢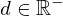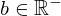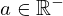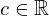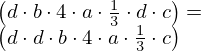
	: , : , : , : , : , : , :
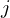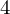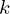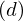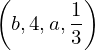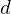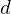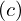11	instantiation	25, 93, 92, 26, 52, 27, 59, 28, 29, 30	, , ,  ⊢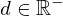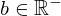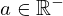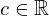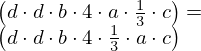
	: , : , : , : , : , : , :
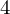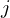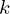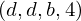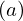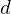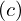12	axiom		⊢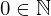
	proveit.numbers.number_sets.natural_numbers.zero_in_nats
13	theorem		⊢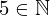
	proveit.numbers.numerals.decimals.nat5
14	theorem		⊢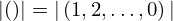
	proveit.core_expr_types.tuples.tuple_len_0_typical_eq
15	instantiation	35	⊢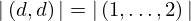
	: , :
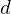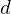16	instantiation	31	⊢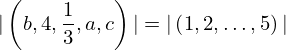
	: , : , : , : , :
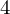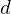17	instantiation	32, 52, 86, 33*, 34*	⊢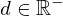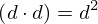
	: , : , :
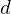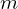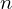18	theorem		⊢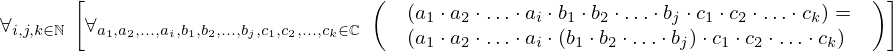
	proveit.numbers.multiplication.association
19	instantiation	35	⊢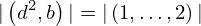
	: , :
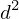20	instantiation	35	⊢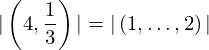
	: , :
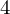21	instantiation	35	⊢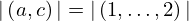
	: , :
22	instantiation	36, 52, 37	⊢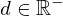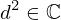
	: , :
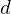23	instantiation	38, 59, 48, 39, 40, 41*, 42*, 43*	⊢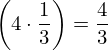
	: , : , : , :
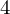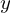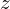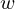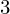24	instantiation	44	⊢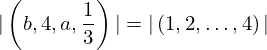
	: , : , : , :
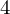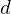25	theorem		⊢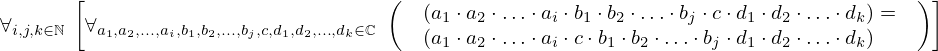
	proveit.numbers.multiplication.leftward_commutation
26	instantiation	44	⊢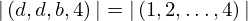
	: , : , : , :
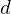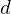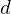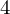27	instantiation	94, 72, 45	⊢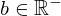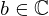
	: , : , :
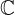28	instantiation	94, 72, 46	⊢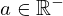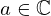
	: , : , :
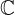29	instantiation	47, 48, 61, 49	⊢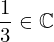
	: , :
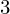30	instantiation	94, 72, 50	⊢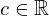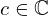
	: , : , :
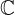31	theorem		⊢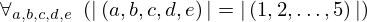
	proveit.numbers.numerals.decimals.tuple_len_5_typical_eq
32	theorem		⊢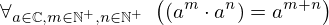
	proveit.numbers.exponentiation.product_of_posnat_powers
33	instantiation	51, 52	⊢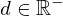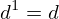
	:
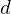34	theorem		⊢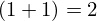
	proveit.numbers.numerals.decimals.add_1_1
35	theorem		⊢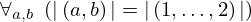
	proveit.numbers.numerals.decimals.tuple_len_2_typical_eq
36	theorem		⊢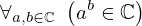
	proveit.numbers.exponentiation.exp_complex_closure
37	instantiation	94, 72, 53	⊢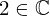
	: , : , :
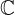38	theorem		⊢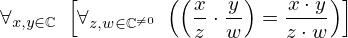
	proveit.numbers.division.prod_of_fracs
39	instantiation	94, 55, 54	⊢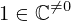
	: , : , :
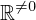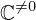40	instantiation	94, 55, 56	⊢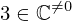
	: , : , :
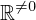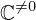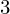41	instantiation	57, 59	⊢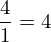
	:
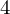42	instantiation	58, 59	⊢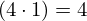
	:
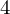43	instantiation	60, 61	⊢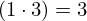
	:
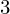44	theorem		⊢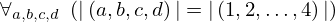
	proveit.numbers.numerals.decimals.tuple_len_4_typical_eq
45	instantiation	94, 75, 62	⊢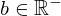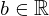
	: , : , :
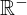46	instantiation	94, 75, 63	⊢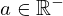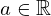
	: , : , :
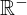47	theorem		⊢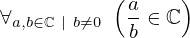
	proveit.numbers.division.div_complex_closure
48	instantiation	94, 72, 64	⊢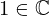
	: , : , :
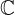49	instantiation	65, 88	⊢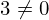
	:
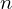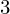50	assumption		⊢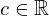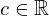
51	theorem		⊢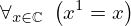
	proveit.numbers.exponentiation.complex_x_to_first_power_is_x
52	instantiation	94, 72, 66	⊢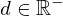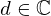
	: , : , :
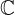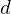53	instantiation	94, 82, 67	⊢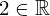
	: , : , :
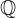54	instantiation	94, 69, 68	⊢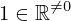
	: , : , :
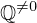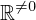55	theorem		⊢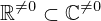
	proveit.numbers.number_sets.complex_numbers.real_nonzero_within_complex_nonzero
56	instantiation	94, 69, 70	⊢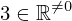
	: , : , :
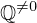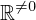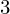57	theorem		⊢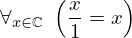
	proveit.numbers.division.frac_one_denom
58	theorem		⊢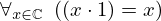
	proveit.numbers.multiplication.elim_one_right
59	instantiation	94, 72, 71	⊢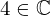
	: , : , :
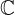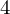60	theorem		⊢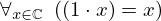
	proveit.numbers.multiplication.elim_one_left
61	instantiation	94, 72, 73	⊢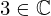
	: , : , :
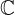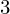62	assumption		⊢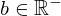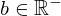
63	assumption		⊢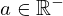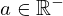
64	instantiation	94, 82, 74	⊢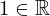
	: , : , :
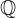65	theorem		⊢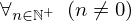
	proveit.numbers.number_sets.natural_numbers.nonzero_if_is_nat_pos
66	instantiation	94, 75, 76	⊢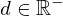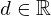
	: , : , :
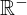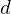67	instantiation	94, 90, 77	⊢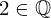
	: , : , :
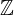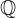68	instantiation	94, 79, 78	⊢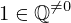
	: , : , :
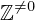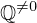69	theorem		⊢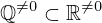
	proveit.numbers.number_sets.real_numbers.rational_nonzero_within_real_nonzero
70	instantiation	94, 79, 80	⊢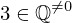
	: , : , :
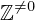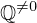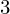71	instantiation	94, 82, 81	⊢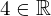
	: , : , :
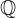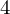72	theorem		⊢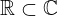
	proveit.numbers.number_sets.complex_numbers.real_within_complex
73	instantiation	94, 82, 83	⊢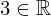
	: , : , :
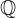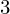74	instantiation	94, 90, 84	⊢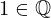
	: , : , :
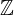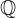75	theorem		⊢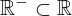
	proveit.numbers.number_sets.real_numbers.real_neg_within_real
76	assumption		⊢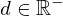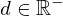
77	instantiation	94, 95, 85	⊢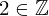
	: , : , :
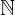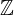78	instantiation	94, 87, 86	⊢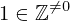
	: , : , :
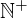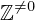79	theorem		⊢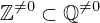
	proveit.numbers.number_sets.rational_numbers.nonzero_int_within_rational_nonzero
80	instantiation	94, 87, 88	⊢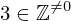
	: , : , :
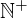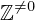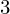81	instantiation	94, 90, 89	⊢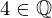
	: , : , :
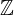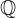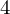82	theorem		⊢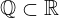
	proveit.numbers.number_sets.real_numbers.rational_within_real
83	instantiation	94, 90, 91	⊢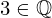
	: , : , :
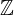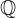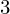84	instantiation	94, 95, 92	⊢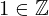
	: , : , :
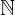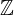85	theorem		⊢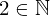
	proveit.numbers.numerals.decimals.nat2
86	theorem		⊢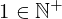
	proveit.numbers.numerals.decimals.posnat1
87	theorem		⊢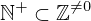
	proveit.numbers.number_sets.integers.nat_pos_within_nonzero_int
88	theorem		⊢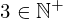
	proveit.numbers.numerals.decimals.posnat3
89	instantiation	94, 95, 93	⊢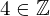
	: , : , :
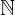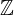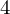90	theorem		⊢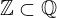
	proveit.numbers.number_sets.rational_numbers.int_within_rational
91	instantiation	94, 95, 96	⊢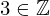
	: , : , :
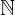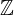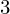92	theorem		⊢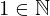
	proveit.numbers.numerals.decimals.nat1
93	theorem		⊢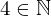
	proveit.numbers.numerals.decimals.nat4
94	theorem		⊢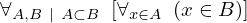
	proveit.logic.sets.inclusion.superset_membership_from_proper_subset
95	theorem		⊢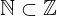
	proveit.numbers.number_sets.integers.nat_within_int
96	theorem		⊢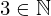
	proveit.numbers.numerals.decimals.nat3
*equality replacement requirements