Computes the Karhunen-Loeve decomposition of a univariate stochastic process.
More...
#include <kle.h >
KLDecompUni (const Array1D < double > &tSamples) Constructor that takes the autocorrelation matrix "corr" ( KLDecompUni () ~KLDecompUni () Destructor. void Init () void SetWeights (const Array1D < double > &weights) Set weights for computing the integral needed for Nystrom's method for solving the Fredholm integral equation. void SetWeights (const double *weights, const int npts) Set weights for computing the integral needed for Nystrom's method for solving the Fredholm integral equation. int decompose (const Array2D < double > &corr, const int &nKL) Perform KL decomposition into nKL modes and return actual number of modes that were obtained. int decompose (const double *corr, const int &nKL) Perform KL decomposition into nKL modes and return actual number of modes that were obtained. void KLproject (const Array2D < double > &realiz, Array2D < double > &xi) Project realizations const Array1D < double > & eigenvalues () const Get eigenvalues in descending order. void eigenvalues (const int nEIG, double *eigs) const const Array2D < double > & KLmodes () const Get associated KL modes. void KLmodes (const int npts, const int nKL, double *klModes) const Get associated KL modes. void meanRealiz (const Array2D < double > &realiz, Array1D < double > &mean_realiz) Calculate (in meanRealiz) the mean realizations. void truncRealiz (const Array1D < double > &meanrea, const Array2D < double > &xi, const int &nKL, Array2D < double > &trunc_realiz) Returns the truncated KL sum.
KLDecompUni (const KLDecompUni &) Dummy default constructor, which should not be used as it is not well defined.
bool decomposed_ Flag to determine whether KL decomposition has taken place (and consequently that the interal data structures contain meaningful eigenvalues and vectors ... ) Array2D < double > whcwh_ Matrix to hold the upper triangular part of the matrix to get eigenvalues of. Array1D < double > w_ Array to hold weights for Nystrom's method for Fredholm integral equation solution. Array1D < double > wh_ Array to hold square roots of weights. char jobz_ Option to determine what to compute (eigenvalues and eigenvectors) char eigRange_ Option to set the type of range for eigenvalues. char uplo_ Option to indicate how matrix is stored. double vl_ Lower bound for range of eigenvalues. double vu_ Upper bound for range of eigenvalues. int il_ Lower index of range of eigenvalues requested. int iu_ Upper index of range of eigenvalues requested. double absTol_ Absolute tolerance for convergence. Array1D < double > eig_values_ Array to store eigenvalues. Array2D < double > KL_modes_ Matrix to store KL modes. int eig_info_ info on success of the eigenvector solutions Array1D < int > ifail_ Array to store indices of eigenvectors that failed to converge.
Computes the Karhunen-Loeve decomposition of a univariate stochastic process.
◆ [1/3]
KLDecompUni::KLDecompUni
(
const Array1D < double > & tSamples )
Constructor that takes the autocorrelation matrix "corr" (
Constructs weights (
◆ [2/3]
KLDecompUni::KLDecompUni
(
)
◆
KLDecompUni::~KLDecompUni
(
)
inline
◆ [3/3]
Dummy default constructor, which should not be used as it is not well defined.
Dummy copy constructor, which should not be used as it is currently not well defined
◆ [1/2]
int KLDecompUni::decompose
(
const Array2D < double > & corr
const int & nKL
◆ [2/2]
int KLDecompUni::decompose
(
const double * corr
const int & nKL
◆ [1/2]
const Array1D < double > & KLDecompUni::eigenvalues
(
)
const
Get eigenvalues in descending order.
◆ [2/2]
void KLDecompUni::eigenvalues
(
const int nEIG
double * eigs
◆
void KLDecompUni::Init
(
)
◆ [1/2]
const Array2D < double > & KLDecompUni::KLmodes
(
)
const
◆ [2/2]
void KLDecompUni::KLmodes
(
const int npts
const int nKL
double * klModes
◆
void KLDecompUni::KLproject
(
const Array2D < double > & realiz
Array2D < double > &xi
Project realizations
Samples of random variables
... or numerically
◆
void KLDecompUni::meanRealiz
(
const Array2D < double > & realiz
Array1D < double > &mean_realiz
Calculate (in meanRealiz) the mean realizations.
◆ [1/2]
void KLDecompUni::SetWeights
(
const Array1D < double > & weights )
Set weights for computing the integral needed for Nystrom's method for solving the Fredholm integral equation.
◆ [2/2]
void KLDecompUni::SetWeights
(
const double * weights
const int npts
Set weights for computing the integral needed for Nystrom's method for solving the Fredholm integral equation.
◆
void KLDecompUni::truncRealiz
(
const Array1D < double > & meanrea
const Array2D < double > & xi
const int & nKL
Array2D < double > &trunc_realiz
Returns the truncated KL sum.
◆
double KLDecompUni::absTol_
private
Absolute tolerance for convergence.
◆
bool KLDecompUni::decomposed_
private
Flag to determine whether KL decomposition has taken place (and consequently that the interal data structures contain meaningful eigenvalues and vectors ... )
◆
int KLDecompUni::eig_info_
private
info on success of the eigenvector solutions
◆
Array1D <double> KLDecompUni::eig_values_
private
Array to store eigenvalues.
◆
char KLDecompUni::eigRange_
private
Option to set the type of range for eigenvalues.
◆
Array to store indices of eigenvectors that failed to converge.
◆
Lower index of range of eigenvalues requested.
◆
Upper index of range of eigenvalues requested.
◆
Option to determine what to compute (eigenvalues and eigenvectors)
◆
Array2D <double> KLDecompUni::KL_modes_
private
Matrix to store KL modes.
◆
Option to indicate how matrix is stored.
◆
Lower bound for range of eigenvalues.
◆
Upper bound for range of eigenvalues.
◆
Array to hold weights for Nystrom's method for Fredholm integral equation solution.
◆
Array to hold square roots of weights.
◆
Array2D <double> KLDecompUni::whcwh_
private
Matrix to hold the upper triangular part of the matrix to get eigenvalues of.
The documentation for this class was generated from the following files:
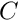
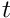
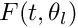
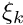
![\[
F(t,\theta) = \left < F(t,\theta) \right >_{\theta}
+ \sum_{k=1}^{\infty} \sqrt{\lambda_k} f_k(t) \xi_k\]](form_72.png)
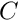
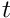
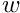
![\[ \int C(s,t)f(t)dt=\lambda f(s) \rightarrow \sum w_j C(s_i,t_j) f_k(t_j) = \lambda_k f_k(s_i)\]](form_76.png)
![\[A g=\lambda g \]](form_77.png)
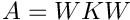
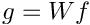
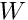
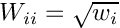
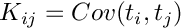
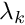
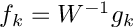
![\[A g=\lambda g \]](form_77.png)
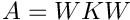
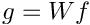
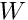
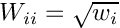
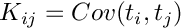
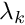
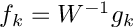
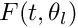
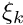
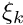
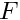
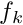
![\[ \left.\xi_k\right\vert_{\theta_l}=\left <F(t,\theta_l)-\left <
F(t,\theta) \right >_{\theta}, f_k(t) \right >_t/\sqrt{\lambda_k} \]](form_89.png)
![\[
\left.\xi_k\right\vert_{\theta_l}=\sum_{i=1}^{N_p} w_i\left(F(t_i,\theta_l)-\left <
F(t_i,\theta) \right >_{\theta} \right) f_k(t_i)/\sqrt{\lambda_k} \]](form_90.png)
![\[
F(t_i,\theta_l) = \left < F(t_i,\theta) \right >_{\theta}
+ \sum_{k=1}^{nKL} \sqrt{\lambda_k} f_k(t_i) \left. \xi_k\right\vert_{\theta_l}
\]](form_91.png)