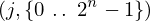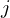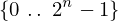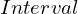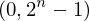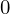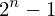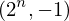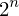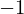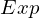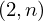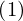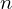Expression of type ExprTuple

from the theory of proveit.physics.quantum.algebra

import proveit
# Automation is not needed when building an expression:
proveit.defaults.automation = False # This will speed things up.
proveit.defaults.inline_pngs = False # Makes files smaller.
%load_expr # Load the stored expression as 'stored_expr'
# import Expression classes needed to build the expression
from proveit import ExprTuple, j
from proveit.physics.quantum.algebra import n_bit_interval

# build up the expression from sub-expressions
expr = ExprTuple(j, n_bit_interval)

expr:

# check that the built expression is the same as the stored expression
assert expr == stored_expr
assert expr._style_id == stored_expr._style_id
print("Passed sanity check: expr matches stored_expr")

Passed sanity check: expr matches stored_expr

# Show the LaTeX representation of the expression for convenience if you need it.
print(stored_expr.latex())

\left(j, \{0~\ldotp \ldotp~2^{n} - 1\}\right)

stored_expr.style_options()

name	description	default	current value	related methods
wrap_positions	position(s) at which wrapping is to occur; 'n' is after the nth comma.	()	()	('with_wrapping_at',)
justification	if any wrap positions are set, justify to the 'left', 'center', or 'right'	left	left	('with_justification',)

# display the expression information
stored_expr.expr_info()

	core type	sub-expressions	expression
0	ExprTuple	1, 2
1	Variable
2	Operation	operator: 3 operands: 4
3	Literal
4	ExprTuple	5, 6
5	Literal
6	Operation	operator: 7 operands: 8
7	Literal
8	ExprTuple	9, 10
9	Operation	operator: 11 operands: 12
10	Operation	operator: 13 operand: 17
11	Literal
12	ExprTuple	15, 16
13	Literal
14	ExprTuple	17
15	Literal
16	Variable
17	Literal