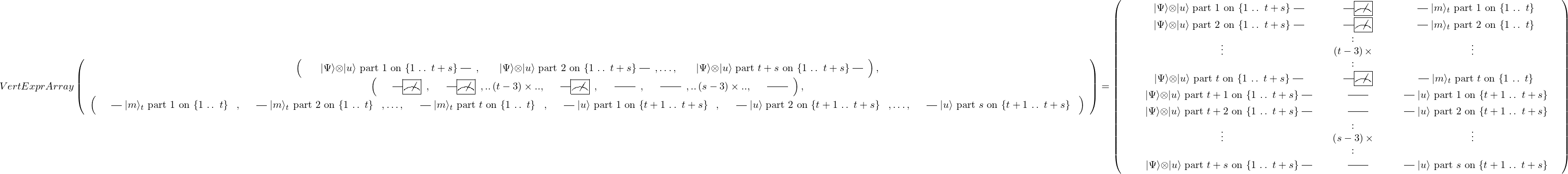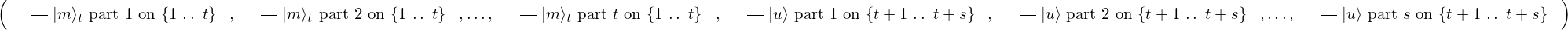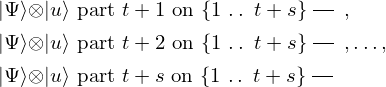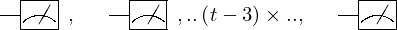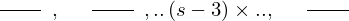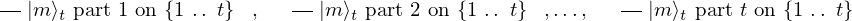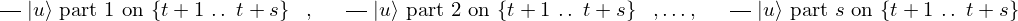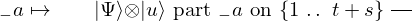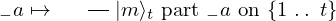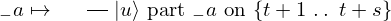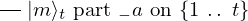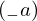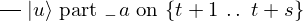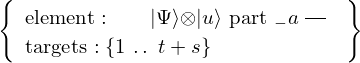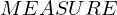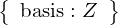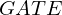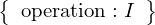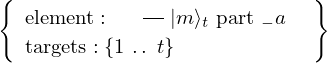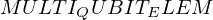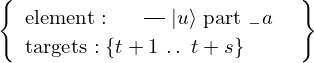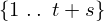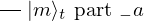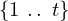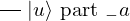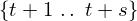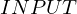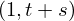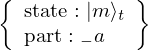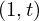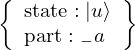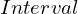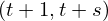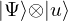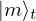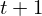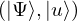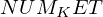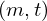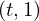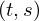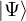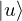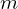logo

Expression of type Equals

from the theory of proveit.physics.quantum.QPE

In [1]:
import proveit
# Automation is not needed when building an expression:
proveit.defaults.automation = False # This will speed things up.
proveit.defaults.inline_pngs = False # Makes files smaller.
%load_expr # Load the stored expression as 'stored_expr'
# import Expression classes needed to build the expression
from proveit import ExprRange, Variable, VertExprArray, m
from proveit.linear_algebra import TensorProd
from proveit.logic import Equals
from proveit.numbers import Add, Interval, one
from proveit.physics.quantum import NumKet, Z
from proveit.physics.quantum.QPE import _Psi_ket, _ket_u, _s, _s_wire, _t
from proveit.physics.quantum.circuits import Input, Measure, MultiQubitElem, Output
In [2]:
# build up the expression from sub-expressions
sub_expr1 = Variable("_a", latex_format = r"{_{-}a}")
sub_expr2 = Add(_t, _s)
sub_expr3 = Add(_t, one)
sub_expr4 = [ExprRange(sub_expr1, Measure(basis = Z), one, _t), _s_wire]
sub_expr5 = MultiQubitElem(element = Input(state = TensorProd(_Psi_ket, _ket_u), part = sub_expr1), targets = Interval(one, sub_expr2))
sub_expr6 = [ExprRange(sub_expr1, MultiQubitElem(element = Output(state = NumKet(m, _t), part = sub_expr1), targets = Interval(one, _t)), one, _t), ExprRange(sub_expr1, MultiQubitElem(element = Output(state = _ket_u, part = sub_expr1), targets = Interval(sub_expr3, sub_expr2)), one, _s)]
expr = Equals(VertExprArray([ExprRange(sub_expr1, sub_expr5, one, sub_expr2)], sub_expr4, sub_expr6), VertExprArray([ExprRange(sub_expr1, sub_expr5, one, _t).with_wrapping_at(2,6), ExprRange(sub_expr1, sub_expr5, sub_expr3, sub_expr2).with_wrapping_at(2,6)], sub_expr4, sub_expr6))
expr:
In [3]:
# check that the built expression is the same as the stored expression
assert expr == stored_expr
assert expr._style_id == stored_expr._style_id
print("Passed sanity check: expr matches stored_expr")

Passed sanity check: expr matches stored_expr
In [4]:
# Show the LaTeX representation of the expression for convenience if you need it.
print(stored_expr.latex())

VertExprArray\left(\begin{array}{c} \left(\begin{array}{c} \Qcircuit@C=1em @R=.7em{
& \qin{\lvert \Psi \rangle {\otimes} \lvert u \rangle~\mbox{part}~1~\mbox{on}~\{1~\ldotp \ldotp~t + s\}} & \qw 
} \end{array}, \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& \qin{\lvert \Psi \rangle {\otimes} \lvert u \rangle~\mbox{part}~2~\mbox{on}~\{1~\ldotp \ldotp~t + s\}} & \qw 
} \end{array}, \ldots, \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& \qin{\lvert \Psi \rangle {\otimes} \lvert u \rangle~\mbox{part}~t + s~\mbox{on}~\{1~\ldotp \ldotp~t + s\}} & \qw 
} \end{array}\right),  \\ \left(\begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \meter 
} \end{array}, \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \meter 
} \end{array}, ..\left(t - 3\right) \times.., \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \meter 
} \end{array},\begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qw & \qw 
} \end{array}, \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qw & \qw 
} \end{array}, ..\left(s - 3\right) \times.., \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qw & \qw 
} \end{array}\right),  \\ \left(\begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qout{\lvert m \rangle_{t}~\mbox{part}~1~\mbox{on}~\{1~\ldotp \ldotp~t\}} 
} \end{array}, \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qout{\lvert m \rangle_{t}~\mbox{part}~2~\mbox{on}~\{1~\ldotp \ldotp~t\}} 
} \end{array}, \ldots, \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qout{\lvert m \rangle_{t}~\mbox{part}~t~\mbox{on}~\{1~\ldotp \ldotp~t\}} 
} \end{array},\begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qout{\lvert u \rangle~\mbox{part}~1~\mbox{on}~\{t + 1~\ldotp \ldotp~t + s\}} 
} \end{array}, \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qout{\lvert u \rangle~\mbox{part}~2~\mbox{on}~\{t + 1~\ldotp \ldotp~t + s\}} 
} \end{array}, \ldots, \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qout{\lvert u \rangle~\mbox{part}~s~\mbox{on}~\{t + 1~\ldotp \ldotp~t + s\}} 
} \end{array}\right) \end{array}\right) = \left(\begin{array}{ccc} 
 \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& \qin{\lvert \Psi \rangle {\otimes} \lvert u \rangle~\mbox{part}~1~\mbox{on}~\{1~\ldotp \ldotp~t + s\}} & \qw 
} \end{array} & \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \meter 
} \end{array} & \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qout{\lvert m \rangle_{t}~\mbox{part}~1~\mbox{on}~\{1~\ldotp \ldotp~t\}} 
} \end{array} \\
\begin{array}{c} \Qcircuit@C=1em @R=.7em{
& \qin{\lvert \Psi \rangle {\otimes} \lvert u \rangle~\mbox{part}~2~\mbox{on}~\{1~\ldotp \ldotp~t + s\}} & \qw 
} \end{array} & \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \meter 
} \end{array} & \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qout{\lvert m \rangle_{t}~\mbox{part}~2~\mbox{on}~\{1~\ldotp \ldotp~t\}} 
} \end{array} \\
\vdots & \begin{array}{c}:\\ \left(t - 3\right) \times \\:\end{array} & \vdots \\
\begin{array}{c} \Qcircuit@C=1em @R=.7em{
& \qin{\lvert \Psi \rangle {\otimes} \lvert u \rangle~\mbox{part}~t~\mbox{on}~\{1~\ldotp \ldotp~t + s\}} & \qw 
} \end{array} & \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \meter 
} \end{array} & \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qout{\lvert m \rangle_{t}~\mbox{part}~t~\mbox{on}~\{1~\ldotp \ldotp~t\}} 
} \end{array} \\
\begin{array}{c} \Qcircuit@C=1em @R=.7em{
& \qin{\lvert \Psi \rangle {\otimes} \lvert u \rangle~\mbox{part}~t + 1~\mbox{on}~\{1~\ldotp \ldotp~t + s\}} & \qw 
} \end{array} & \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qw & \qw 
} \end{array} & \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qout{\lvert u \rangle~\mbox{part}~1~\mbox{on}~\{t + 1~\ldotp \ldotp~t + s\}} 
} \end{array} \\
\begin{array}{c} \Qcircuit@C=1em @R=.7em{
& \qin{\lvert \Psi \rangle {\otimes} \lvert u \rangle~\mbox{part}~t + 2~\mbox{on}~\{1~\ldotp \ldotp~t + s\}} & \qw 
} \end{array} & \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qw & \qw 
} \end{array} & \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qout{\lvert u \rangle~\mbox{part}~2~\mbox{on}~\{t + 1~\ldotp \ldotp~t + s\}} 
} \end{array} \\
\vdots & \begin{array}{c}:\\ \left(s - 3\right) \times \\:\end{array} & \vdots \\
\begin{array}{c} \Qcircuit@C=1em @R=.7em{
& \qin{\lvert \Psi \rangle {\otimes} \lvert u \rangle~\mbox{part}~t + s~\mbox{on}~\{1~\ldotp \ldotp~t + s\}} & \qw 
} \end{array} & \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qw & \qw 
} \end{array} & \begin{array}{c} \Qcircuit@C=1em @R=.7em{
& & \qout{\lvert u \rangle~\mbox{part}~s~\mbox{on}~\{t + 1~\ldotp \ldotp~t + s\}} 
} \end{array} \\
\end{array}
\right)
In [5]:
stored_expr.style_options()
namedescriptiondefaultcurrent valuerelated methods
operation'infix' or 'function' style formattinginfixinfix
wrap_positionsposition(s) at which wrapping is to occur; '2 n - 1' is after the nth operand, '2 n' is after the nth operation.()()('with_wrapping_at', 'with_wrap_before_operator', 'with_wrap_after_operator', 'without_wrapping', 'wrap_positions')
justificationif any wrap positions are set, justify to the 'left', 'center', or 'right'centercenter('with_justification',)
directionDirection of the relation (normal or reversed)normalnormal('with_direction_reversed', 'is_reversed')
In [6]:
# display the expression information
stored_expr.expr_info()
 core typesub-expressionsexpression
0Operationoperator: 1
operands: 2
1Literal
2ExprTuple3, 4
3ExprTuple5, 7, 8
4ExprTuple6, 7, 8
5ExprTuple9
6ExprTuple10, 11
7ExprTuple12, 13
8ExprTuple14, 15
9ExprRangelambda_map: 16
start_index: 67
end_index: 56
10ExprRangelambda_map: 16
start_index: 67
end_index: 68
11ExprRangelambda_map: 16
start_index: 55
end_index: 56
12ExprRangelambda_map: 17
start_index: 67
end_index: 68
13ExprRangelambda_map: 18
start_index: 67
end_index: 69
14ExprRangelambda_map: 19
start_index: 67
end_index: 68
15ExprRangelambda_map: 20
start_index: 67
end_index: 69
16Lambdaparameter: 54
body: 21
17Lambdaparameter: 54
body: 22
18Lambdaparameter: 54
body: 23
19Lambdaparameter: 54
body: 24
20Lambdaparameter: 54
body: 26
21Operationoperator: 33
operands: 27
22Operationoperator: 28
operands: 29
23Operationoperator: 30
operands: 31
24Operationoperator: 33
operands: 32
25ExprTuple54
26Operationoperator: 33
operands: 34
27NamedExprselement: 35
targets: 36
28Literal
29NamedExprsbasis: 37
30Literal
31NamedExprsoperation: 38
32NamedExprselement: 39
targets: 40
33Literal
34NamedExprselement: 41
targets: 42
35Operationoperator: 43
operands: 44
36Operationoperator: 50
operands: 45
37Literal
38Literal
39Operationoperator: 48
operands: 46
40Operationoperator: 50
operands: 47
41Operationoperator: 48
operands: 49
42Operationoperator: 50
operands: 51
43Literal
44NamedExprsstate: 52
part: 54
45ExprTuple67, 56
46NamedExprsstate: 53
part: 54
47ExprTuple67, 68
48Literal
49NamedExprsstate: 65
part: 54
50Literal
51ExprTuple55, 56
52Operationoperator: 57
operands: 58
53Operationoperator: 59
operands: 60
54Variable
55Operationoperator: 62
operands: 61
56Operationoperator: 62
operands: 63
57Literal
58ExprTuple64, 65
59Literal
60ExprTuple66, 68
61ExprTuple68, 67
62Literal
63ExprTuple68, 69
64Literal
65Literal
66Variable
67Literal
68Literal
69Literal