sibl
Lesson 08: Swiss cheese
The SIBL Mesh Engine can be used with multiple curve definitions.
Goals
Demonstrate mesh creation for a domain with an inner and outer boundary definitions.
Steps
SIBL Mesh engine can import boundary files with multiple loops specified.
- It assumes that distinct loops are separted by
NaNvalues forxandyvalues. - It also uses the convention that a counter clockwise loop defines a region
that is “IN” and should be meshed, while a clockwise loop specifies a region
that is “OUT” and should not be meshed. For example, the
NaNappears in line85ofswisscheese.txt, used in the example below, as shown in this screenshot:
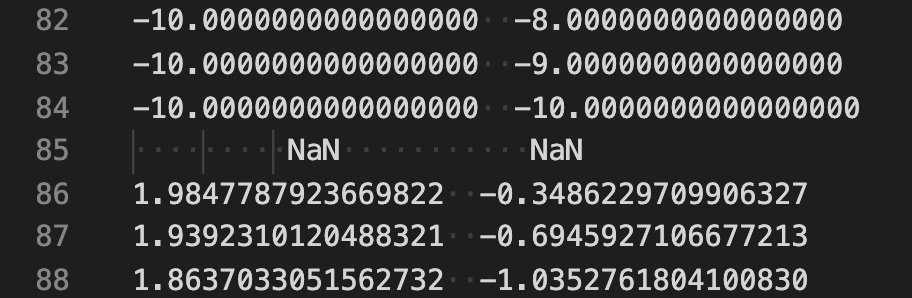
Figure 12.1: Illustration of the use of
NaNto incidate termination of a curve and start of a new curve.
Boundary File Generation
This boundary specification is create with the MATLAB
plotSwissCheeseEx.m file. The important
distinction for this file versus other plot commands is that this handles the
tris and pents that appear in the Primal mesh. The .dev files just pad the
poly specification with -1s. So there is a line in the MATLAB code that strips
out the -1 indices before plotting.
The swisscheese.yml configuration file is also
used as an input to dual.exe.
clear all
close all
%Set path to executable if not working in the same directory
binpath = 'C:\Users\acsokol\sibl\geo\src\dual\bin\';
%Create the geometry for this example
%Make a box
edge1 = [-10:1:10];
edge2 = edge1*0+1;
xp = [edge1 edge2*10 edge1(end:-1:1) -edge2*10];
yp = [-edge2*10 edge1 edge2*10 edge1(end:-1:1)];
%Make some cutout circles
th = [0:5:355];
xp2 = 4*cosd(th)-2;
yp2 = 4*sind(th);
xp =[xp NaN xp2(end:-1:1)];
yp =[yp NaN yp2(end:-1:1)];
xp2 = 2*cosd(th)+5;
yp2 = 2*sind(th)+3;
xp =[xp NaN xp2(end:-1:1)];
yp =[yp NaN yp2(end:-1:1)];
xp2 = 3*cosd(th)+1;
yp2 = 3*sind(th)-6;
xp =[xp NaN xp2(end:-1:1)];
yp =[yp NaN yp2(end:-1:1)];
pts = [xp' yp']';
%Write geometry to file
fid = fopen(['swisscheese.txt'],'w');
fprintf(fid,'%12.16f %12.16f\n',pts);
fclose(fid);
% Create a text file named swisscheese.yml, that contains the following lines or run executable with no args to get a template yml file
% boundary:swisscheese.txt
% boundary_refine:true
% bounding_box:-10,-10,10,10
% developer_output:true
% output_file:swiss
% resolution:1
% version:1.1
%Run executable through Matlab dos command / Can also just drag YML file onto executable or run from command prompt
dos([binpath,'dual.exe swisscheese.yml']);
plotNames = {'_01_quad_tree_','_02_primal_','_03_dual_','_04_d_trim_','_05_dt_project_','_06_dtp_snap_','_07_dtps_subdivide_','_08_dtpss_project_','_09_dtpssp_snap_','_10_mesh_'};
for ff=1:length(plotNames)
n = load(['swisscheese',char(plotNames{ff}),'nodes.dev']);
q = load(['swisscheese',char(plotNames{ff}),'quads.dev']);
figure;
plot(pts(1,:),pts(2,:),'k-','LineWidth',2);hold on;
for qq=1:size(q,1)
seq = q(qq,:);
seq = seq(seq~=-1);
seq = [seq seq(1)]; %close the loops
plot(n(seq,2),n(seq,3),'k-')
end
axis equal;
axis off
title(char(plotNames{ff}))
print(gcf,'-dpng',['swiss',char(plotNames{ff}),'.png']);
end
Quad Tree
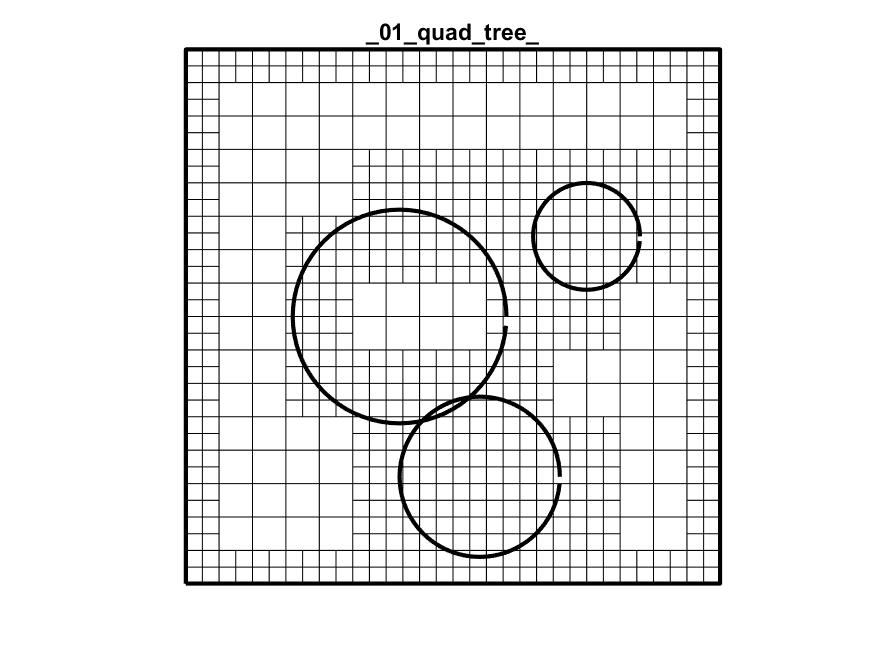
Primal
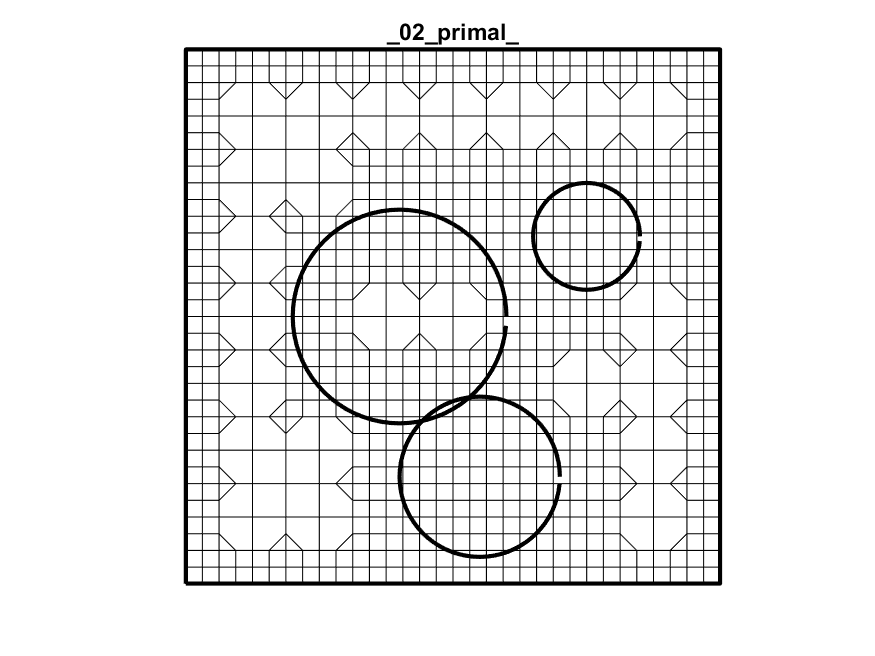
Primal + Dual
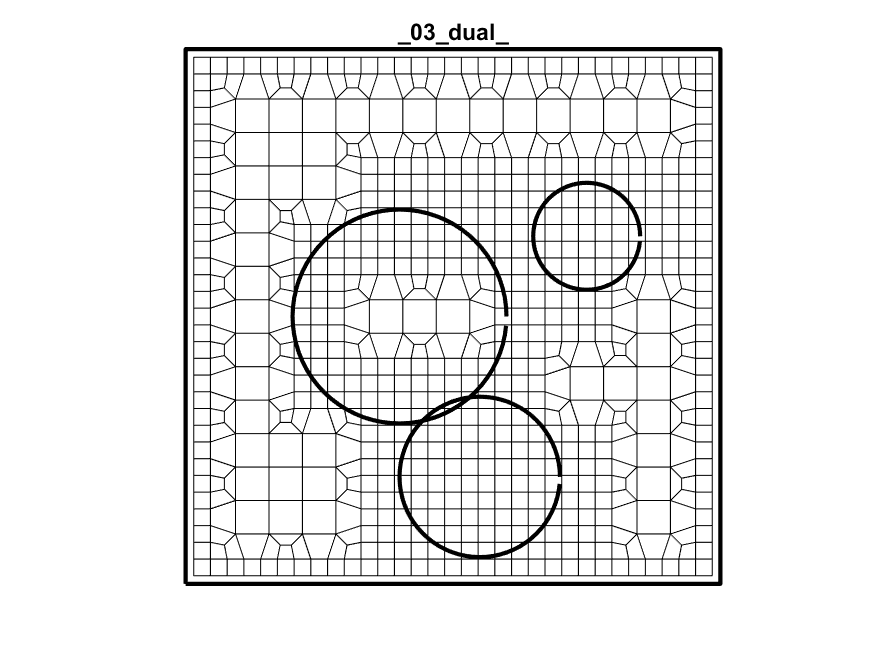
Dual + Trim + Project
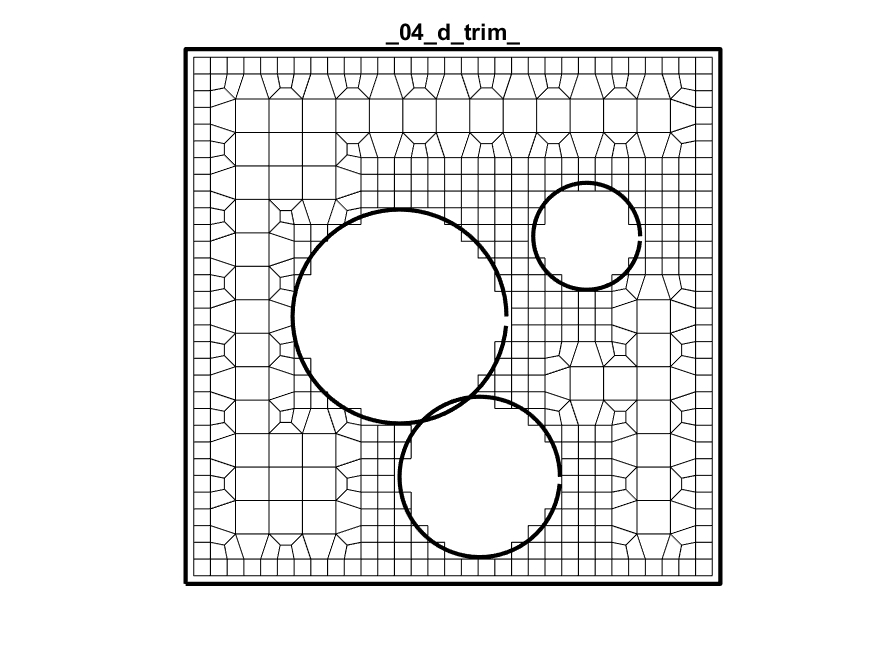
Dual + Trim + Project
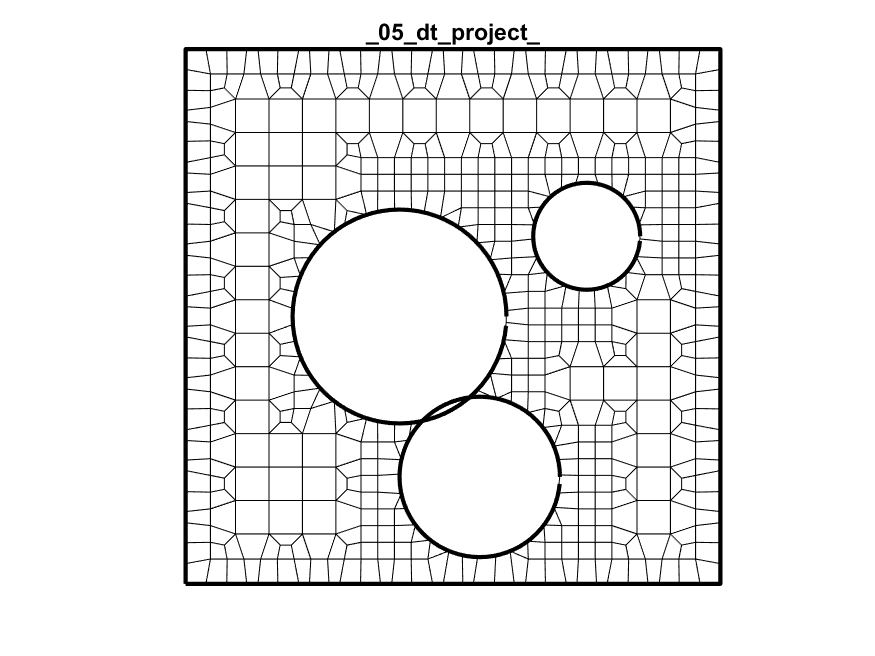
Dual + Trim + Project + Snap
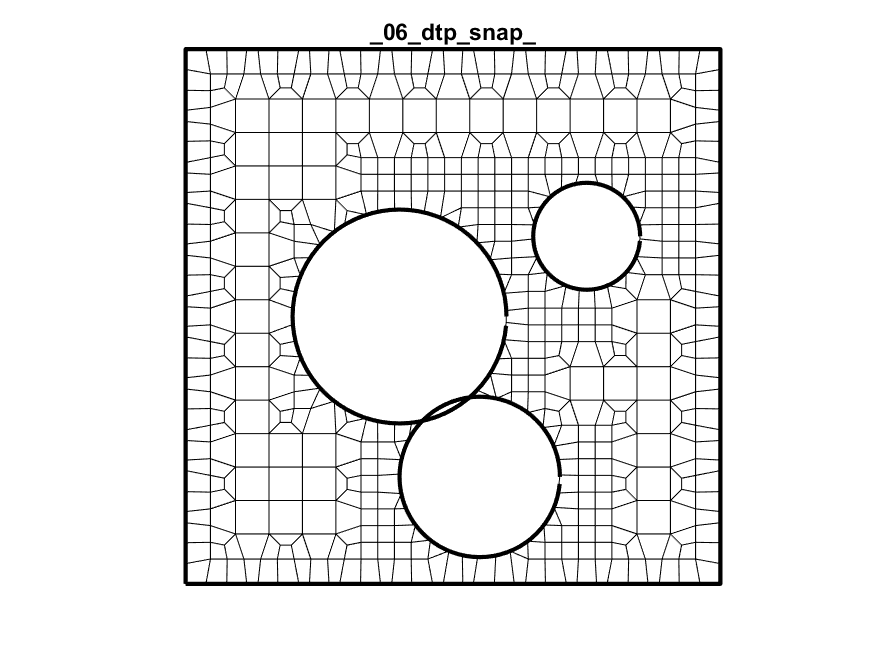
Dual + Trim + Project + Snap + Subdivide
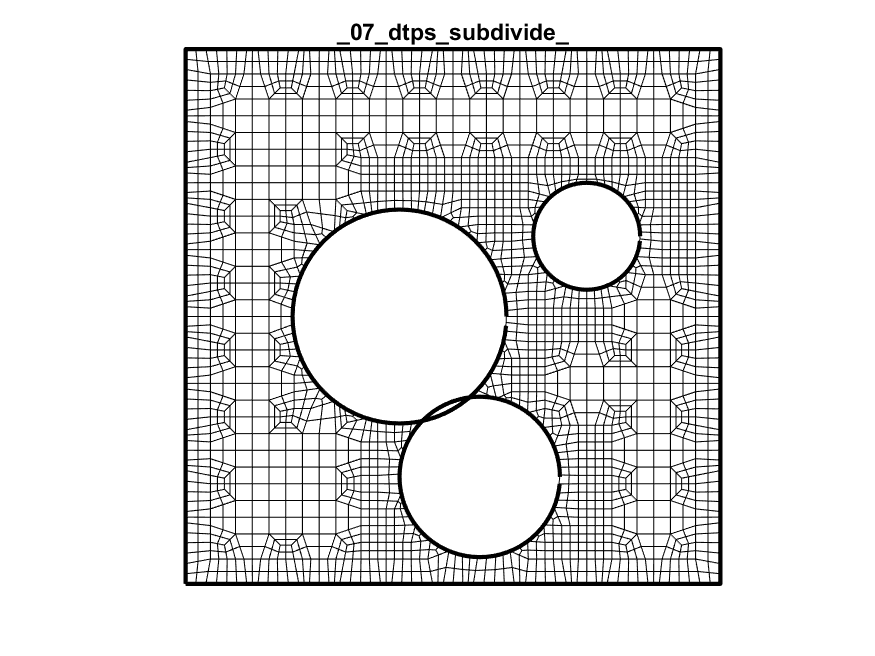
Dual + Trim + Project + Snap + Subdivide + Project
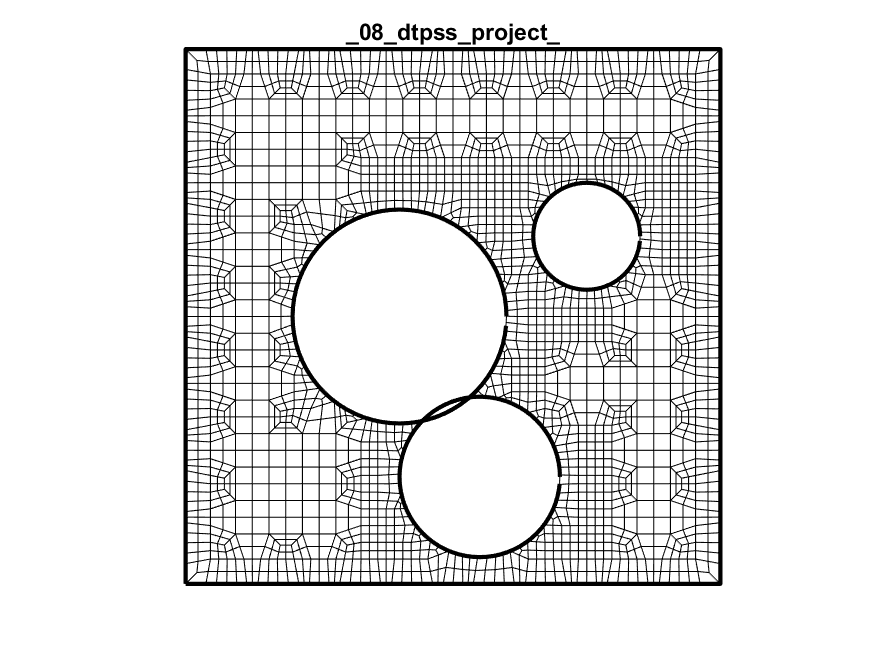
Dual + Trim + Project + Snap + Subdivide + Project + Snap
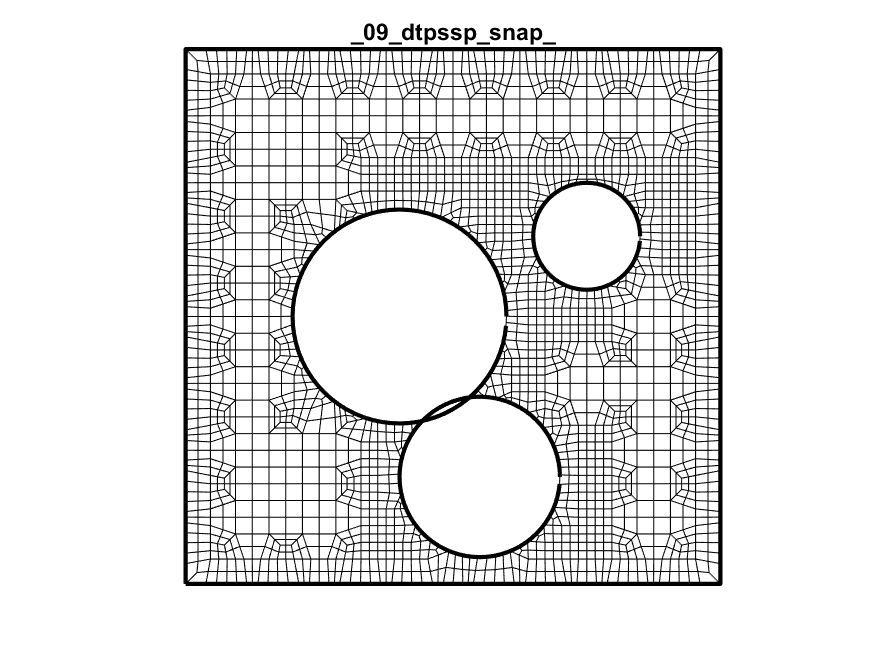
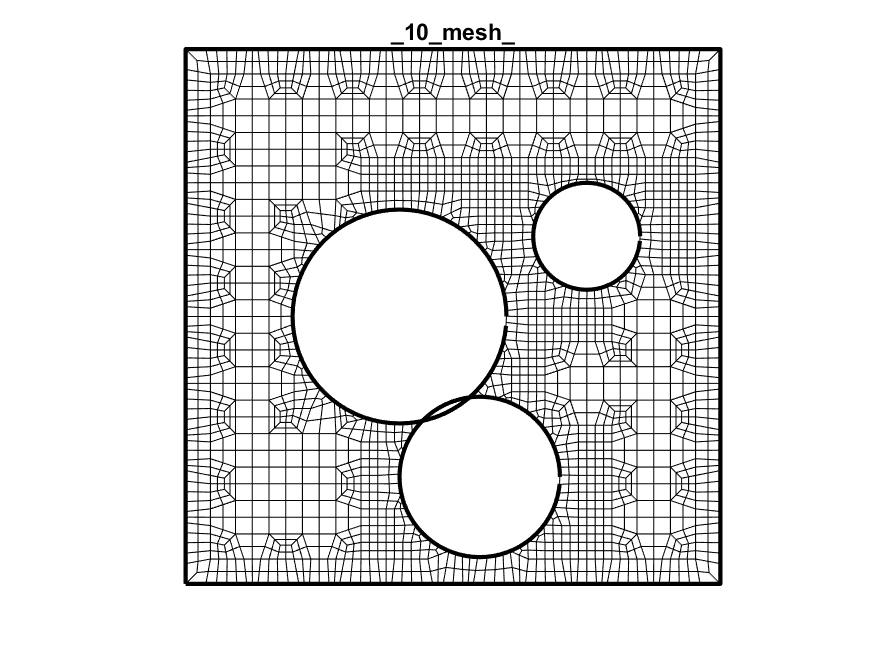
Final Mesh
Previous: Lesson 07