sibl

Integration

Important Note: The initial conditions are in units of the native signal. Therefore, if the native signal will be scaled (e.g., going from m/s^2 to G or vice versa), care must be taken on the units of the initial conditions. The initial conditions are applied before any scaling.

Constant Function

• constant zero jerk (m/s^3) with zeros.json:
• then triple integration with initial conditions:
  • u''(0) = -10 m/s^2
  • u'(0) = 100 m/s
  • u(0) = 1000 m

Implemented with zeros-int3.json, resulting in zeros-int3.png 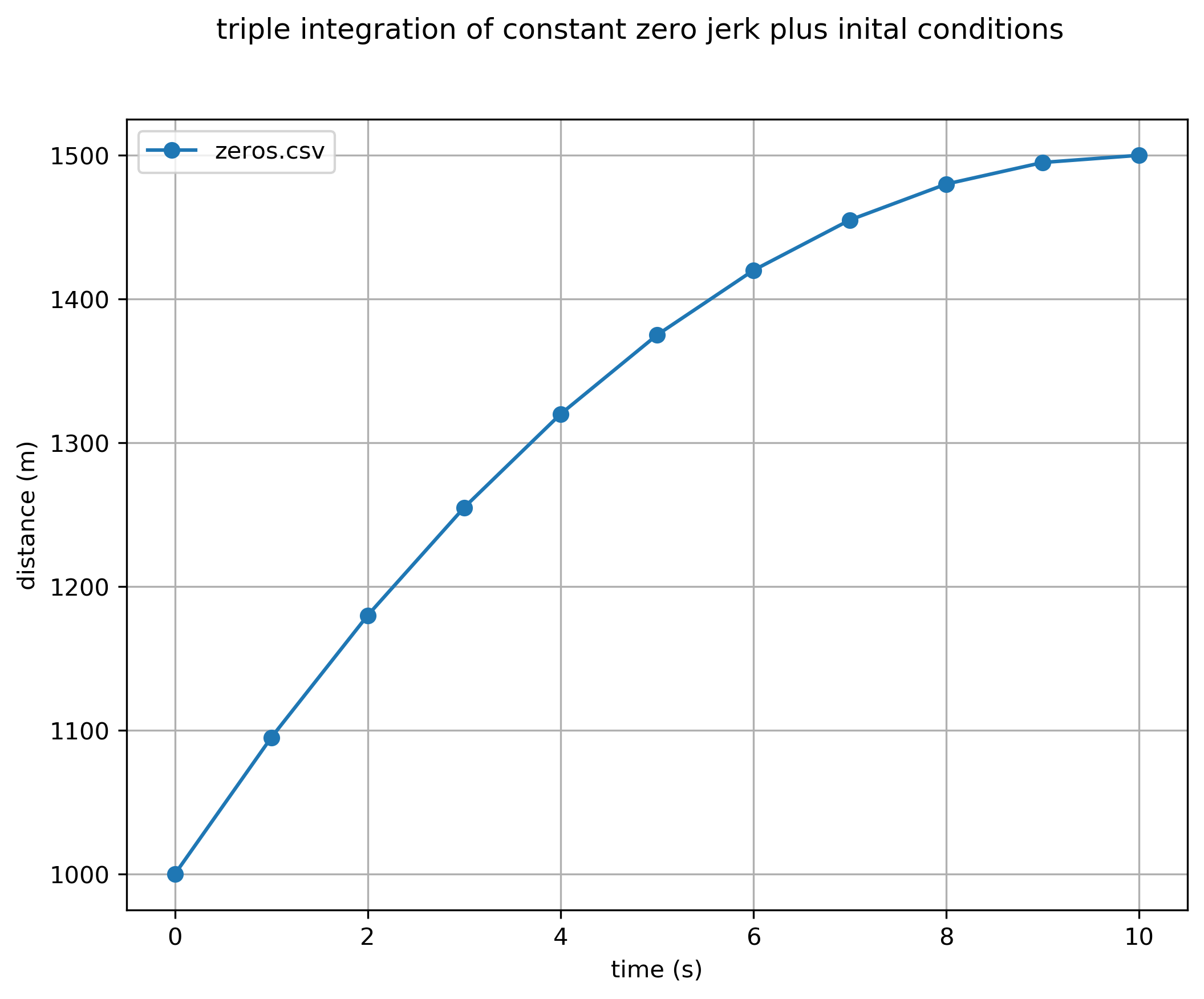and the signal process output file (triple integration of jerk to get displacement) as zeros-int3.csv.

The closed form solution for the acceleration is

• u''(t) = int(u''') dt + u''(0) = -10 * [1 1 1 1 1 1 1 1 1 1 1] m/s^2
• -----> = -10 m/s^2

The closed form solution for the velocity is

• u'(t) = int(u'') dt + u'(0) = -10 [0 1 2 3 4 5 6 7 8 9 10] + 100 m/s
• ----> = -10*t + 100 m/s
• ----> = [100 90 80 70 60 50 40 30 20 10 0] m/s

The closed form solution for the displacement is

• u(t) = int(u') dt + u(0)
• ---> = -5*t^2 + 100*t + 1000 m
• ---> = 1000 + [0 95 180 255 320 375 420 455 480 495 500]

This site is open source. Improve this page.