Project Motivation
The Zoltan Toolkit
Terminology
Zoltan Design
However, increasing use of "dynamic" simulation techniques is creating new challenges for developers of parallel software. For example, adaptive finite element methods refine localized regions the mesh and/or adjust the order of the approximation on individual elements to obtain a desired accuracy in the numerical solution. As a result, memory must be allocated dynamically to allow creation of new elements or degrees of freedom. Communication patterns can vary as refinement creates new element neighbors. And localized refinement can cause severe processor load imbalance as elemental and processor work loads change throughout a simulation.
Particle simulations and crash simulations are other examples of dynamic applications. In particle simulations, scalable parallel performance depends upon a good assignment of particles to processors; grouping physically close particles within a single processor reduces inter-processor communication. Similarly, in crash simulations, assignment of physically close surfaces to a single processor enables efficient parallel contact search. In both cases, data structures and communication patterns change as particles and surfaces move. Re-partitioning of the particles or surfaces is needed to maintain geometric locality of objects within processors.
We developed the Zoltan library to simplilfy many of the difficulties arising in dynamic applications. Zoltan is a collection of data management services for unstructured, adaptive and dynamic applications. It includes a suite of parallel partitioning algorithms, data migration tools, parallel graph coloring tools, distributed data directories, unstructured communication services, and dynamic memory management tools. Zoltan's data-structure neutral design allows it to be used by a variety of applications without imposing restrictions on application data structures. Its object-based interface provides a simple and inexpensive way for application developers to use the library and researchers to make new capabilities available under a common interface.
Each object must have a unique global identifier (ID) represented as an array of unsigned integers. Common choices include global numbers of elements (nodes, particles, rows, and so on) that already exist in many applications, or a structure consisting of an owning processor number and the object's local-memory index. Objects might also have local (to a processor) IDs that do not have to be unique globally. Local IDs such as addresses or local-array indices of objects can improve the performance (and convenience) of Zoltan's interface to applications.
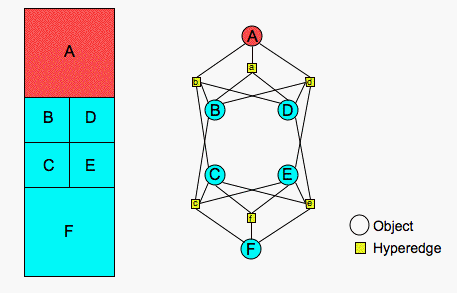
We use a simple example to illustrate the above terminology. On the left side of the figure below, a simple finite element mesh is presented.

The blue and red shading indicates the mesh is partitioned for two processors. An application must provide information about the current mesh and partition to Zoltan. If, for example, the application wants Zoltan to perform operations on the elements of the mesh, it must provide information about the elements when Zoltan asks for object information.
In this example, the elements have unique IDs assigned to them, as shown by the letters in the elements. These unique letters can be used as global IDs in Zoltan. In addition, on each processor, local numbering information may be available. For instance, the elements owned by a processor may be stored in arrays in the processor's memory. An element's local array index may be provided to Zoltan as a local ID.
For geometric algorithms, the application must provide coordinate information to Zoltan. In this example, the coordinates of the mid-point of an element are used.
For hypergraph- and graph-based algorithms, information about the connectivity of the objects must be provided to Zoltan. In this example, the application may consider elements connected if they share a face. A hypergraph representing this problem is then shown to the right of the mesh. A hyperedge exists for each object (squares labeled with lower-case letters corresponding to the related object). Each hyperedge connects the object and all of its face neighbors. The hyperedges are passed to Zoltan with a label (in this example, a lower-case letter) and a list of the object IDs in that hyperedge.
Graph connections, or edges, across element faces may also specified. Connectivity information is passed to Zoltan by specifying a neighbor list for an object. The neighbor list consists of the global IDs of neighboring objects and the processor(s) currently owning those objects. Because relationships across faces are bidirectional, the graph edge lists and hypergraph hyperedge lists are nearly identical. If, however, information flowed to, say, only the north and east edge neighbors of an element, the hypergraph model would be needed, as the graph model can represent only bidirectional relationships. In this case, the hyperedge contents would include only the north and east neighbors; they would exclude south and west neighbors.
The table below summarizes the information provided to Zoltan by an application for this finite element mesh. Information about the objects includes their global and local IDs, geometry data, hypergraph data, and graph data.
To keep the application interface simple, we use a small set of callback functions and make them easy to write by requesting only information that is easily accessible to applications. For example, the most basic partitioning algorithms require only four callback functions. These functions return the number of objects owned by a processor, a list of weights and IDs for owned objects, the problem's dimensionality, and a given object's coordinates. More sophisticated graph-based partitioning algorithms require only two additional callback functions, which return the number of edges per object and edge lists for objects.