Hierarchical Partitioning (HIER)

Partitioning to the hierarchy of a distributed system is described below. Employing callbacks to the user at each level, Zoltan will balance the problem across platforms of varying capabilities while minimizing communication along slower links.

Partitioning an application to run on a multicore machine, where the multicore nodes are expected to be homogeneous in architecture, is described in the next section. Using a parameter supplied by the application which describes node topology, Zoltan will partition the problem to balance computation while minimizing inter-node communication, and communication between on-node structures.

Hierarchical Partitioning for multicore machines

Some limitations of this method to note are that Zoltan assumes:

• Each node (processor) of the multicore machine has the same architecture.
• The MPI process ranks are consecutive on the multicore nodes.

In particular, if your parameters imply there are 4 MPI processes on each multicore node, Zoltan will assume that processes 0, 1, 2 and 3 are on the same node. Your system administrator should be able to show you how to ensure that your processes are loaded in this order.

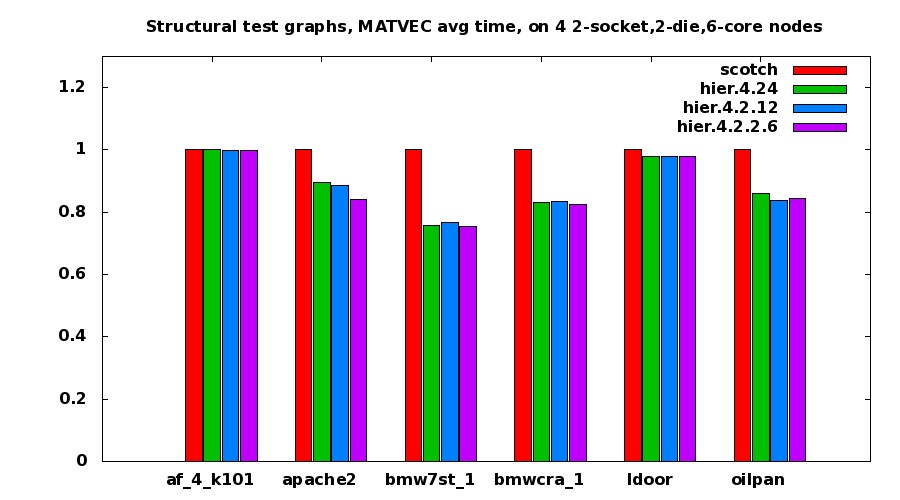
The results shown below emphasize that the benefit to be gained from levels of hierarchical partitioning is very dependent on the commmunication patterns of the problem.

These results show the runtime for matrix vector multiplication for some matrices from the University of Florida matrix collection. The tests were run on four nodes of the Hopper machine at NERSC, a machine composed of dual-socket, dual-die nodes, with each die having 6 cores. The graphs were first partitioned once across all 96 processes with PTScotch. Then, using hierarchical partitioning with TOPOLOGY="24", they were partitioned across the nodes first, then the cores. Then with TOPOLOGY="2,12" they were partitioned across the nodes, then across the sockets, then into 12 parts. Finally, with TOPOLOGY="2,2,6" they were partitioned across the nodes, then the sockets, then the dies, and finally partitioned into 6 parts. (Runtime is normalized to the flat partitioning case.)

 

Method String:	HIER
Parameters:
HIER_ASSIST	Setting this parameter to 1 indicates that the application wishes Zoltan to perform hierarchcial partitioning for homogeneous multicore nodes, without requiring the application to supply query functions guiding the partitioning.
TOPOLOGY	This comma-separated list of integers describes the topology of the multicore node. For example: "2,8" may refer to a dual-socket processor where each socket has 8 cores. "2,4,6" may refer to a dual-socket, 4-die, 6-core node "16" would refer to a 16-core node
HIER_DEBUG_LEVEL	0 = no debugging output 1 = show hierarchy and MPI ranks for each part at each level 2 = in addition, all processes print status information at each level
Default:
	HIER_ASSIST = 1 if TOPOLOGY is defined, 0 otherwise
	TOPOLOGY has no default value.
	HIER_DEBUG_LEVEL = 0
Required Query Functions:	There are no query functions required specifically for hierarchical partitioning to multicore nodes. If the application supplies geometric query functions then Zoltan will use RIB partitioning at each level, using whatever relevant parameters the application has set. If the application supplies graph query functions, then Zoltan will perform graph partitioning at each level, again using whatever relevant graph partitioning parameters the application has set.

Hierarchical Partitioning for distributed computing

Zoltan's hierarchical balancing, implemented by Jim Teresco (Williams College) during a 2003-04 visit to Sandia, automates the creation of hierarchical partitions [Teresco, et al.]. It can be used directly by an application or be guided by the tree representation of the computational environment created and maintained by the Dynamic Resource Utilization Model (DRUM) [Devine, et al. , Faik, et al., Teresco, et al.].

The hierarchical balancing implementation utilizes a lightweight intermediate structure and a set of callback functions that permit an automated and efficient hierarchical balancing which can use any of the procedures available within Zoltan without modification and in any combination. Hierachical balancing is invoked by an application the same way as other Zoltan procedures and interfaces with applications through callback functions. A hierarchical balancing step begins by building an intermediate structure using these callbacks. This structure is an augmented version of the graph structure that Zoltan builds to make use of the ParMetis and Jostle libraries. The hierarchical balancing procedure then provides its own callback functions to allow existing Zoltan procedures to be used to query and update the intermediate structure at each level of a hierarchical balancing. After all levels of the hierarchical balancing have been completed, Zoltan's usual migration arrays are constructed and returned to the application. Thus, only lightweight objects are migrated internally between levels, not the (larger and more costly) application data.

Hierarchical partitioning requires three callback functions to specify the number of levels (ZOLTAN_HIER_NUM_LEVELS_FN), which parts each process should compute at each level (ZOLTAN_HIER_PART_FN), and which method and parameters to be used at each level (ZOLTAN_HIER_METHOD_FN). These are in addition to the callbacks needed to specify objects, coordinates, and graph edges. This fairly cumbersome interface can be avoided by using the separately available zoltanParams library. This allows a file-based description to replace these callbacks. A more direct interface with DRUM's hierarchical machine model is also planned, allowing hierarchical balancing parameters to be set by a graphical configuration tool.

We use a simple example to illustrate the use of the callback mechanism to specify hierarchical a hierarchical partitioning. In the figure below, a hierarchical computing environment and a desired hierarchical partitioning is shown.

Assume we start one process for each processor, with the processes of ranks 0-3 assigned to Node 0, 4-7 to Node 1, 8-11 to Node 2, and 12-15 to Node 3. When hierarchical partitioning is invoked, the following callbacks will be made, and the following actions should be taken by the callbacks on each node.

1. The ZOLTAN_HIER_NUM_LEVELS_FN callback is called. All processes should return 2, the number of levels in the hierarchy.
2. The ZOLTAN_HIER_PART_FN callback is called, with a level parameter equal to 0. This means the callback should return, on each process, the part number to be computed at level 0 by that process. Since in our example, the 16 processes are computing a four-way partition at level 0, processes with ranks 0-3 should return 0, ranks 4-7 should return 1, 8-11 should return 2, and 12-15 should return 3.
3. The ZOLTAN_HIER_METHOD_FN callback is called, with a level parameter equal to 0, and the Zoltan_Struct that has been allocated internally by the hierarchical partitioning procedure is passed as zz. The callback should use Zoltan_Set_Param to specify an LB_METHOD and any other parameters that should be done by the four-way partition across the 16 processes at level 0. In this case, two calls might be appropriate:

     Zoltan_Set_Param(zz, "LB_METHOD", "PARMETIS");
     Zoltan_Set_Param(zz, "PARMETIS_METHOD", "PARTKWAY");
   

   At this point, Zoltan's hierarchical balancing procedure can proceed with the level 0 partition, using ParMetis' PARTKWAY method to produce a four-way partition across the 16 processes, with part 0 distributed among the processes with ranks 0-3, part 1 distributed among 4-7, part 2 distributed among 8-11, and part 3 distributed among 12-15.
4. The ZOLTAN_HIER_PART_FN callback is called again, this time with level equal to 1. At level 1, each group of four processes on the same node is responsible for computing its own four-way partition. To specify this, processes with ranks 0, 4, 8, and 12 should return 0, ranks 1, 5, 9, and 13 should return 1, ranks 2, 6, 10, and 14 should return 2, and ranks 3, 7, 11, and 15 should return 3. Note that we are specifying four separate four-way partitions at this level, so each group of four processes on the same node will have one process computing each part 0, 1, 2, and 3, for that group.
5. The ZOLTAN_HIER_METHOD_FN callback is called again, with level equal to 1, and another internally-allocated Zoltan_Struct passed as zz. Here, we want all processes to be computing a partition using recursive inertial bisection. The following call would be appropriate inside the callback:

     Zoltan_Set_Param(zz, "LB_METHOD", "RIB");
   

   Additional Zoltan_Set_Param calls would be used to specify any additional procedures. Note that in this case, we are computing four separate partitions but all with the same LB_METHOD. It would be allowed to specify different LB_METHODs for each group, but all processes cooperating on a partition must agree on their LB_METHOD and other parameters (just like any other Zoltan partitioning).

   At this point, Zoltan's hierarchical balancing procedure can proceed with the level 1 partition, using four independent recursive inertial bisections produce the four four-way partitions across the processes on each node. Since this is the final level, the 16 resulting parts are returned by the hierarchical balancing procedure to the calling application.