Header for tools related to Rosenblatt transformation. More...
Go to the source code of this file.
Functions | |
| void | invRos (Array1D< double > &unif, Array2D< double > &xi, Array1D< double > &newXi, Array1D< double > &sig) |
| Generates a new sample by inverse Rosenblatt defined by a given sample set (xi) and a 'uniform' sample from the unit hypercube. | |
| void | invRos (Array1D< double > &unif, Array2D< double > &xi, Array1D< double > &newXi, double bw) |
| This is a version of invRos() with the same bandwidth (bw) for all dimensions. | |
| void | invRos (Array1D< double > &unif, Array2D< double > &xi, Array1D< double > &newXi) |
| This is a version of invRos() with an automatic bandwidth selection based on a rule of thumb. | |
| void | invRos (Array2D< double > &unif, Array2D< double > &xi, Array2D< double > &newXi) |
| This is a version of invRos() with an automatic bandwidth selection based on a rule of thumb, and operating on set of uniform samples (rather than one at a time) | |
| void | get_opt_KDEbdwth (const Array2D< double > &data, Array1D< double > &bdwth) |
| Calculates 'rule of thumb' optimal KDE bandwidths for a multi-dimensional data. | |
| void | Rosen (Array2D< double > &xi, Array2D< double > &xi_data, Array2D< double > &unif, Array1D< double > &sig) |
| Given input samples (xi), generates uniform samples by Rosenblatt map whose PDF is defined by a given sample set (xi_data) | |
| void | Rosen (Array2D< double > &xi, Array2D< double > &xi_data, Array2D< double > &unif, double bw) |
| This is a version of Rosen() with the same bandwidth (bw) for all dimensions. | |
| void | Rosen (Array2D< double > &xi, Array2D< double > &xi_data, Array2D< double > &unif) |
| This is a version of Rosen() with an automatic bandwidth selection based on a rule of thumb. | |
Detailed Description
Header for tools related to Rosenblatt transformation.
Function Documentation
◆ get_opt_KDEbdwth()
Calculates 'rule of thumb' optimal KDE bandwidths for a multi-dimensional data.
- Note
- Employs Silverman's rule-of-thumb, with a homemade factor adjustment accounting for samples that are near boundaries
- This rule-of-thumb is quite heuristic; use at your own risk
- Parameters
-
[in] data : 2-dimensional array of size 
[out] bdwth : 1-dimensional array of size 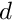
◆ invRos() [1/4]
This is a version of invRos() with an automatic bandwidth selection based on a rule of thumb.
- Note
- The rule of thumb is not always reliable. It is recommended to test various bandwidths.
◆ invRos() [2/4]
| void invRos | ( | Array1D< double > & | unif, |
| Array2D< double > & | xi, | ||
| Array1D< double > & | newXi, | ||
| Array1D< double > & | sig ) |
Generates a new sample by inverse Rosenblatt defined by a given sample set (xi) and a 'uniform' sample from the unit hypercube.
- Note
- Performs inverse Rosenblatt map
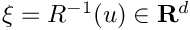
![$u\in[0,1]^d$](form_63.png)
- The command line utility app/pce_quad uses this map; see UQTk Manual entry for the app for technical description of the map
- Parameters
-
[in] unif : 1-dimensional array of size 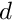
![$u\in[0,1]^d$](form_63.png)
[in] xi : 2-dimensional array of size 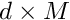
[out] newXi : 1-dimensional array of size 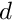
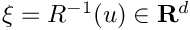
[in] sig : 1-dimensional array of size 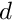
◆ invRos() [3/4]
| void invRos | ( | Array1D< double > & | unif, |
| Array2D< double > & | xi, | ||
| Array1D< double > & | newXi, | ||
| double | bw ) |
This is a version of invRos() with the same bandwidth (bw) for all dimensions.
◆ invRos() [4/4]
This is a version of invRos() with an automatic bandwidth selection based on a rule of thumb, and operating on set of uniform samples (rather than one at a time)
- Parameters
-
[in] unif : 2-dimensional array of size 
![$u\in[0,1]^d$](form_63.png)
[in] xi : 2-dimensional array of size 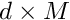
[out] newXi : 2-dimensional array of size 
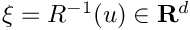
- Note
- The rule of thumb is not always reliable. It is recommended to test various bandwidths.
◆ Rosen() [1/3]
This is a version of Rosen() with an automatic bandwidth selection based on a rule of thumb.
- Note
- The rule of thumb is not always reliable. It is recommended to test various bandwidths.
◆ Rosen() [2/3]
| void Rosen | ( | Array2D< double > & | xi, |
| Array2D< double > & | xi_data, | ||
| Array2D< double > & | unif, | ||
| Array1D< double > & | sig ) |
Given input samples (xi), generates uniform samples by Rosenblatt map whose PDF is defined by a given sample set (xi_data)
- Note
- Performs Rosenblatt map
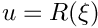
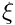
- Parameters
-
[in] xi : 2-dimensional array of size 
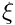
[in] xi_data : 2-dimensional array of size 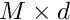
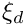
[out] unif : 2-dimensional array of size 
![$[0,1]^d$](form_71.png)
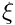
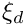
[in] sig : 1-dimensional array of size 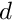
◆ Rosen() [3/3]
Generated by