Implements several functions of form 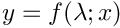$y=f(\lambda;x)$ . More...

#include <math.h>
#include <cfloat>
#include <assert.h>
#include "func.h"
#include "gen_defs.h"
#include "PCSet.h"
#include "error_handlers.h"
#include "arrayio.h"
#include "arraytools.h"

Functions
Array2D< double >	Func_Prop (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
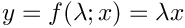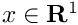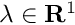	$y=f(\lambda;x)=\lambda x$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^1$

Array2D< double >	Func_PropQuad (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
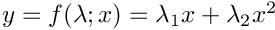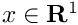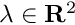	$y=f(\lambda;x)=\lambda_1 x+\lambda_2x^2$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^2$

Array2D< double >	Func_Exp (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
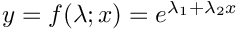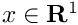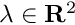	$y=f(\lambda;x)=e^{\lambda_1 +\lambda_2x}$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^2$

Array2D< double >	Func_ExpQuad (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
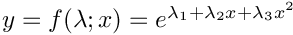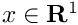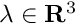	$y=f(\lambda;x)=e^{\lambda_1 +\lambda_2x+\lambda_3x^2}$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^3$

Array2D< double >	Func_Const (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
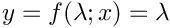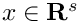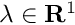	$y=f(\lambda;x)=\lambda$ for $x\in\mathbf{R}^s$ and $\lambda\in\mathbf{R}^1$

Array2D< double >	Func_Linear (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
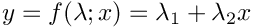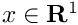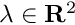	$y=f(\lambda;x)=\lambda_1+\lambda_2x$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^2$

Array2D< double >	Func_BB (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
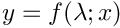	$y=f(\lambda;x)$ a black-box function with a script bb.x which takes p.dat and x.dat and returns output in y.dat

Array2D< double >	Func_HT1 (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
	Heat_transfer1: a custom model designed for a tutorial case of a heat conduction problem.

Array2D< double >	Func_HT2 (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
	Heat_transfer2: a custom model designed for a tutorial case of a heat conduction problem.

Array2D< double >	Func_FracPower (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
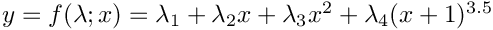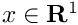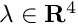	$y=f(\lambda;x)=\lambda_1+\lambda_2 x+\lambda_3 x^2+ \lambda_4 (x+1)^{3.5}$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^4$

Array2D< double >	Func_ExpSketch (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
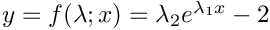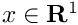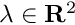	$y=f(\lambda;x)=\lambda_2 e^{\lambda_1 x} - 2$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^2$

Array2D< double >	Func_Inputs (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
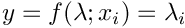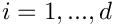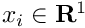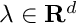	$y=f(\lambda;x_i)=\lambda_i$ for , $x_i\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^d$

Array2D< double >	Func_PCl (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
	Legendre PC expansion with 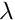$\lambda$ 's as coefficients.

Array2D< double >	Func_PCx (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
	Legendre PC expansion with respect to 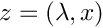$z=(\lambda,x)$ .

Array2D< double >	Func_PC (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
	Legendre PC expansion for each value of .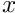

Array2D< double >	Func_PCs (Array2D< double > &p, Array2D< double > &x, Array2D< double > &fixindnom, void *funcinfo)
	Legendre PC expansion for each value of .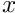

Array2D< double >	augment (Array2D< double > &p, Array2D< double > &fixindnom)
	Augments a parameter matrix with 'fixed' columns given indices and nominal values of those.

Detailed Description

Implements several functions of form 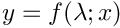$y=f(\lambda;x)$ .

Function Documentation

◆ augment()

Array2D< double > augment	(	Array2D< double > &	p,
		Array2D< double > &	fixindnom )

Augments a parameter matrix with 'fixed' columns given indices and nominal values of those.

◆ Func_BB()

Array2D< double > Func_BB	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

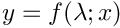
$y=f(\lambda;x)$ a black-box function with a script bb.x which takes p.dat and x.dat and returns output in y.dat

◆ Func_Const()

Array2D< double > Func_Const	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

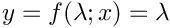
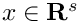
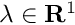
$y=f(\lambda;x)=\lambda$ for $x\in\mathbf{R}^s$ and $\lambda\in\mathbf{R}^1$

◆ Func_Exp()

Array2D< double > Func_Exp	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

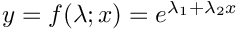
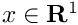
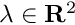
$y=f(\lambda;x)=e^{\lambda_1 +\lambda_2x}$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^2$

◆ Func_ExpQuad()

Array2D< double > Func_ExpQuad	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

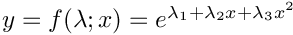
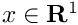
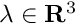
$y=f(\lambda;x)=e^{\lambda_1 +\lambda_2x+\lambda_3x^2}$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^3$

◆ Func_ExpSketch()

Array2D< double > Func_ExpSketch	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

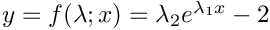
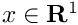
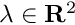
$y=f(\lambda;x)=\lambda_2 e^{\lambda_1 x} - 2$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^2$

◆ Func_FracPower()

Array2D< double > Func_FracPower	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

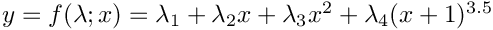
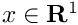
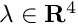
$y=f(\lambda;x)=\lambda_1+\lambda_2 x+\lambda_3 x^2+ \lambda_4 (x+1)^{3.5}$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^4$

◆ Func_HT1()

Array2D< double > Func_HT1	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

Heat_transfer1: a custom model designed for a tutorial case of a heat conduction problem.

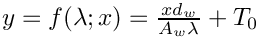
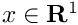
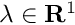
$y=f(\lambda;x)=\frac{x d_w}{A_w \lambda}+T_0$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^1$

Note: hardwired parameters:

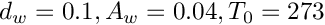
◆ Func_HT2()

Array2D< double > Func_HT2	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

Heat_transfer2: a custom model designed for a tutorial case of a heat conduction problem.

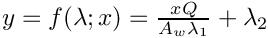
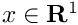
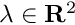
$y=f(\lambda;x)=\frac{x Q}{A_w \lambda_1}+\lambda_2$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^2$

Note: hardwired parameters:

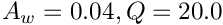
◆ Func_Inputs()

Array2D< double > Func_Inputs	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

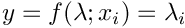
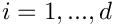
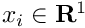
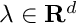
$y=f(\lambda;x_i)=\lambda_i$ for $i=1,...,d$ , $x_i\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^d$

◆ Func_Linear()

Array2D< double > Func_Linear	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

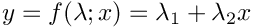
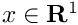
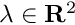
$y=f(\lambda;x)=\lambda_1+\lambda_2x$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^2$

◆ Func_PC()

Array2D< double > Func_PC	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

Legendre PC expansion for each value of 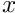$x$ .

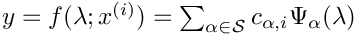
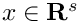
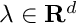
$y=f(\lambda;x^{(i)})=\sum_{\alpha\in{\cal S}} c_{\alpha,i} \Psi_\alpha(\lambda)$ for $x\in\mathbf{R}^s$ and $\lambda\in\mathbf{R}^d$

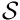
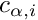
Note: hardwired parameters: common multiindex set for all PCs ${\cal S}$ is given in a file mindexp.dat, coefficients $c_{\alpha,i}$ are given in a file pccf_all.dat

◆ Func_PCl()

Array2D< double > Func_PCl	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

Legendre PC expansion with 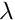$\lambda$ 's as coefficients.

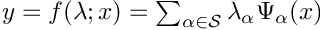
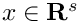
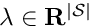
$y=f(\lambda;x)=\sum_{\alpha\in{\cal S}} \lambda_\alpha \Psi_\alpha(x)$ for $x\in\mathbf{R}^s$ and $\lambda\in\mathbf{R}^{|{\cal S}|}$

Note: hardwired parameter: multiindex set ${\cal S}$ is given in a file mindexx.dat

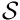
◆ Func_PCs()

Array2D< double > Func_PCs	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

Legendre PC expansion for each value of 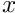$x$ .

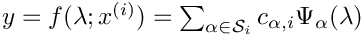
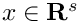
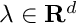
$y=f(\lambda;x^{(i)})=\sum_{\alpha\in{\cal S}_i} c_{\alpha,i} \Psi_\alpha(\lambda)$ for $x\in\mathbf{R}^s$ and $\lambda\in\mathbf{R}^d$

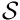
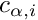
Note: hardwired parameters: multiindex sets for all PCs ${\cal S}$ are given in files mindexp.i.dat, coefficients $c_{\alpha,i}$ are given in files pccfp.i.dat

◆ Func_PCx()

Array2D< double > Func_PCx	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

Legendre PC expansion with respect to 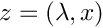$z=(\lambda,x)$ .

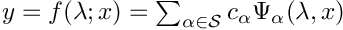
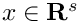
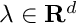
$y=f(\lambda;x)=\sum_{\alpha\in{\cal S}} c_\alpha \Psi_\alpha(\lambda,x)$ for $x\in\mathbf{R}^s$ and $\lambda\in\mathbf{R}^d$

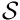
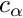
Note: hardwired parameters: multiindex set ${\cal S}$ is given in a file mindexpx.dat, coefficients $c_\alpha$ given in a file pccfpx.dat

◆ Func_Prop()

Array2D< double > Func_Prop	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

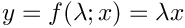
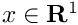
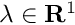
$y=f(\lambda;x)=\lambda x$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^1$

◆ Func_PropQuad()

Array2D< double > Func_PropQuad	(	Array2D< double > &	p,
		Array2D< double > &	x,
		Array2D< double > &	fixindnom,
		void *	funcinfo )

$y=f(\lambda;x)=\lambda_1 x+\lambda_2x^2$ for $x\in\mathbf{R}^1$ and $\lambda\in\mathbf{R}^2$

Functions