Tools to manipulate Array 1D and 2D objects. Some tools mimick MATLAB functionalities. More...

#include "stdlib.h"
#include "stdio.h"
#include "math.h"
#include "assert.h"
#include <sstream>
#include <fstream>
#include <iomanip>
#include "arraytools.h"
#include "ftndefs.h"
#include "gen_defs.h"
#include "depblas.h"
#include "deplapack.h"

Functions
template<typename T >
void	array1Dto2D (Array1D< T > &arr_1d, Array2D< T > &arr)
	Store a given 1d array in a 2d array with a single second dimension.

template void	array1Dto2D (Array1D< double > &arr_1d, Array2D< double > &arr)

template void	array1Dto2D (Array1D< int > &arr_1d, Array2D< int > &arr)

template<typename T >
void	array2Dto1D (Array2D< T > &arr_2d, Array1D< T > &arr)
	Store a given 2d array with a single second dimension in a 1d array.

template void	array2Dto1D (Array2D< double > &arr_2d, Array1D< double > &arr)

template void	array2Dto1D (Array2D< int > &arr_2d, Array1D< int > &arr)

template<typename T >
void	paste (Array1D< T > &arr1, Array1D< T > &arr2, Array2D< T > &arr)
	Paste two 1d arrays of same size into a single 2d array with second dimension equal to two.

template void	paste (Array1D< double > &arr1, Array1D< double > &arr2, Array2D< double > &arr)

template void	paste (Array1D< int > &arr1, Array1D< int > &arr2, Array2D< int > &arr)

template<typename T >
void	generate_multigrid (Array2D< T > &multigrid, Array2D< T > &grid)
	Generates multigrid as a cartesian product of each column of grid.

template void	generate_multigrid (Array2D< double > &multigrid, Array2D< double > &grid)

template void	generate_multigrid (Array2D< int > &multigrid, Array2D< int > &grid)

void	paste (Array2D< double > &x, Array2D< double > &y, Array2D< double > &xy)
	Paste two 2D arrays next to each other (horizontal stack)

void	merge (Array2D< double > &x, Array2D< double > &y, Array2D< double > &xy)
	Merge 2d double arrays (vertical stack)

void	merge (Array1D< double > &x, Array1D< double > &y, Array1D< double > &xy)
	Merge 1d double arrays.

void	merge (Array1D< int > &x, Array1D< int > &y, Array1D< int > &xy)
	Merge 1d int arrays.

void	append (Array1D< double > &x, Array1D< double > &y)
	Append array y to array x in place (double format)

void	append (Array1D< int > &x, Array1D< int > &y)
	Append array y to array x in place (int format)

template<typename T >
void	transpose (Array2D< T > &x, Array2D< T > &xt)
	Transpose a 2d double or int array x and return the result in xt.

template void	transpose (Array2D< double > &x, Array2D< double > &xt)

template void	transpose (Array2D< int > &x, Array2D< int > &xt)

void	flatten (Array2D< double > &arr_2, Array1D< double > &arr_1)
	Unfold/flatten a 2d array into a 1d array (double format)

void	fold_1dto2d_rowfirst (Array1D< double > &x1, Array2D< double > &x2)
	Fold a 1d array into a 2d array (double format), row first.

void	fold_1dto2d_colfirst (Array1D< double > &x1, Array2D< double > &x2)
	Fold a 1d array into a 2d array (double format), column first.

void	swap (Array1D< double > &arr, int i, int j)
	Swap i-th and j-th elements of the array arr.

void	swap (Array2D< double > &arr, int i, int j)
	Swap i-th and j-th rows of the 2d array arr.

double	access (int nx, int ny, Array1D< double > &arr_1, int i, int j)
	Access element 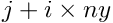$j+i\times ny$ from 1D array 'arr_1'.

double	accessPythonHelper (int nx, int ny, Array1D< double > &arr_1, int i, int j)
	Function written exclusively for Pybind11 to be able to load in the function access.

template<typename T >
void	getRow (Array2D< T > &arr2d, int k, Array1D< T > &arr1d)
	Retrieves row 'k' from 2D array 'arr2d' and returns it in 1D array 'arr1d'.

template void	getRow (Array2D< double > &arr2d, int k, Array1D< double > &arr1d)

template void	getRow (Array2D< int > &arr2d, int k, Array1D< int > &arr1d)

template<typename T >
void	getCol (Array2D< T > &arr2d, int k, Array1D< T > &arr1d)
	Retrieves column 'k' from 2D array 'arr2d' and returns it in 1D array 'arr1d'.

template void	getCol (Array2D< double > &arr2d, int k, Array1D< double > &arr1d)

template void	getCol (Array2D< int > &arr2d, int k, Array1D< int > &arr1d)

template<typename T >
void	addVal (int n, T *arr1d, T val)
	Adds 'val' to the first n elements of an array pointer (double or int)

template void	addVal (int n, double *arr1d, double val)

template void	addVal (int n, int *arr1d, int val)

template<typename T >
void	addVal (Array1D< T > &arr1d, T val)
	Adds 'val' to all elements of 1D array arr1d (double or int)

template void	addVal (Array1D< double > &arr1d, double val)

template void	addVal (Array1D< int > &arr1d, int val)

template<typename T >
void	addVal (Array2D< T > &arr2d, T val)
	Adds 'val' to all elements of 2D array arr2d (double or int)

template void	addVal (Array2D< double > &arr2d, double val)

template void	addVal (Array2D< int > &arr2d, int val)

template<typename T >
void	subVector (Array1D< T > &vector, Array1D< int > &ind, Array1D< T > &subvector)
	Extracts from 'vector', elements corresponding to indices 'ind' and returns them in 'subvector' (double or int)

template void	subVector (Array1D< double > &vector, Array1D< int > &ind, Array1D< double > &subvector)

template void	subVector (Array1D< int > &vector, Array1D< int > &ind, Array1D< int > &subvector)

template<typename T >
void	subMatrix_row (Array2D< T > &matrix, Array1D< int > &ind, Array2D< T > &submatrix)
	Extracts from 'matrix' rows corresponding to indices 'ind' and returns them in 'submatrix' (double or int)

template void	subMatrix_row (Array2D< double > &matrix, Array1D< int > &ind, Array2D< double > &submatrix)

template void	subMatrix_row (Array2D< int > &matrix, Array1D< int > &ind, Array2D< int > &submatrix)

template<typename T >
void	subMatrix_col (Array2D< T > &matrix, Array1D< int > &ind, Array2D< T > &submatrix)
	Extracts from 'matrix' columns corresponding to indices 'ind' and returns them in 'submatrix' (double or int)

template void	subMatrix_col (Array2D< double > &matrix, Array1D< int > &ind, Array2D< double > &submatrix)

template void	subMatrix_col (Array2D< int > &matrix, Array1D< int > &ind, Array2D< int > &submatrix)

template<typename T >
void	matPvec (Array2D< T > &matrix, const Array1D< T > &rc, T alpha, char *RC)
	Adds scaled row or column to all rows / columns of a matrix (double or int)

template void	matPvec (Array2D< double > &matrix, const Array1D< double > &rc, double alpha, char *RC)

template void	matPvec (Array2D< int > &matrix, const Array1D< int > &rc, int alpha, char *RC)

template<typename T >
T	maxVal (const Array1D< T > &vector, int *indx)
	Returns maximum value in 'vector' and its location in *indx (double or int)

template double	maxVal (const Array1D< double > &vector, int *indx)

template int	maxVal (const Array1D< int > &vector, int *indx)

void	setdiff (Array1D< int > &A, Array1D< int > &B, Array1D< int > &C)
	Returns 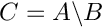$C=A\backslash B$ (C=Elements of A that are not in B); C is sorted in ascending order.

void	setdiff_s (Array1D< int > &A, Array1D< int > &B, Array1D< int > &C)
	Returns 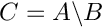$C=A\backslash B$ ( C=Elements of A that are not in B); C is sorted in ascending order.

void	shell_sort (int *a, int n)
	Sorts integer array.

void	shell_sort (Array1D< int > &array)
	Sorts integer array in ascending order.

void	shell_sort (Array1D< double > &array)
	Sorts double array in ascending order.

void	shell_sort_col (Array2D< double > &array, int col, Array1D< int > &newInd, Array1D< int > &oldInd)
	Sorts double array in ascending order according to a given column.

void	shell_sort_all (Array2D< double > &array, Array1D< int > &newInd, Array1D< int > &oldInd)
	Sorts double array in ascending order according to first column, then second column breaks the tie, and so on.

void	quicksort3 (Array1D< double > &arr, int l, int r)
	Quick-sort with 3-way partitioning of array between indices l and r.

void	quicksort3 (Array2D< double > &arr, int l, int r, int col)
	Quick-sort with 3-way partitioning of 2d array between indices l and r, according to column col.

void	quicksort3 (Array2D< double > &arr, int l, int r)
	Quick-sort with 3-way partitioning of 2d array between indices l and r, and sorting is done comparing rows (by first element, then by second, etc...)

void	intersect (Array1D< int > &A, Array1D< int > &B, Array1D< int > &C, Array1D< int > &iA, Array1D< int > &iB)
	Finds common entries in 1D arrays 'A' and 'B' and returns them in 'C', sorted in ascending order. It also returns the original locations of these entries in 1D arrays 'iA' and 'iB', respectively.

void	intersect (Array1D< int > &A, Array1D< int > &B, Array1D< int > &C)
	Find common entries in 1D arrays 'A' and 'B' and return them in 'C', sorted in ascending order.

template<typename T >
void	find (Array1D< T > &theta, T lmbda, string type, Array1D< int > &indx)
	Return list of indices corresponding to elements of 1D array theta that are: larger ( type="gt" ), larger or equal ( type="ge" ), smaller ( type="lt" ), smaller or equal ( type="le" ) than lmbda.

template void	find (Array1D< double > &theta, double lmbda, string type, Array1D< int > &indx)

template void	find (Array1D< int > &theta, int lmbda, string type, Array1D< int > &indx)

void	prodAlphaMatVec (Array2D< double > &A, Array1D< double > &x, double alpha, Array1D< double > &y)
	Returns 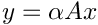$y=\alpha Ax$ , where 'A' is a $\left[n\times m\right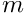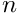]$ 2D array, 'x' is 1D array of size and 'alpha' is a scalar. The 1D array 'y' has elements.

void	prodAlphaMatTVec (Array2D< double > &A, Array1D< double > &x, double alpha, Array1D< double > &y)
	Returns 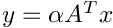$y=\alpha A^Tx$ , where 'A' is a $\left[m\times n\right]$ 2D array, 'x' is 1D array of size and 'alpha' is a scalar. The 1D array 'y' has elements.

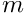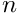void	prodAlphaMatMat (Array2D< double > &A, Array2D< double > &B, double alpha, Array2D< double > &C)
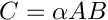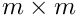	Returns $C=\alpha AB$ , where 'A' and 'B' are $\left[m\times n\right]$ 2D arrays and 'alpha' is a scalar. The 2D array 'C' has $m\times m$ elements.

void	prodAlphaMatTMat (Array2D< double > &A, Array2D< double > &B, double alpha, Array2D< double > &C)
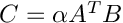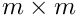	Returns $C=\alpha A^TB$ , where 'A' and 'B' are $\left[m\times n\right]$ 2D arrays and 'alpha' is a scalar. The 2D array 'C' has $m\times m$ elements.

void	addVecAlphaVecPow (Array1D< double > &x, double alpha, Array1D< double > &y, int ip)
	Implements 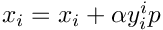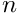$x_i=x_i+\alpha y_i^ip$ , where 'x' and 'y' are 1D arrays with elements.

double	prod_vecTmatvec (Array1D< double > &a, Array2D< double > &B, Array1D< double > &c)
	Returns .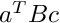

Array2D< double >	MatTMat (Array2D< double > &A)
	Returns 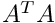, where 'A' is a $\left[n\times k\right]$ 2D array.

template<typename T >
void	delRow (Array2D< T > &A, int irow)
	Deletes row 'irow' from 2D array 'A'.

template void	delRow (Array2D< double > &A, int irow)

template void	delRow (Array2D< int > &A, int irow)

template<typename T >
void	delCol (Array2D< T > &A, int icol)
	Deletes column 'icol' from 2D array 'A'.

template void	delCol (Array2D< double > &A, int icol)

template void	delCol (Array2D< int > &A, int icol)

template<typename T >
void	delCol (Array1D< T > &x, int icol)
	Deletes element 'icol' from 1D array 'A'.

template void	delCol (Array1D< double > &x, int icol)

template void	delCol (Array1D< int > &x, int icol)

void	paddMatRow (Array2D< double > &A, Array1D< double > &x)
	Padds 2D array 'A' with the row 'x'.

void	paddMatCol (Array2D< double > &A, Array1D< double > &x)
	Padds 2D array 'A' with the column 'x'.

void	paddMatRow (Array2D< int > &A, Array1D< int > &x)
	Padds 2D array 'A' with the row 'x'.

void	paddMatCol (Array2D< int > &A, Array1D< int > &x)
	Padds 2D array 'A' with the column 'x'.

void	paddMatColScal (Array2D< double > &A, Array1D< double > &x, double scal)
	Padds square 2D array 'A' $\left[n\times n\right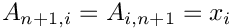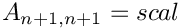]$ with the elements of 'x' and 'scal' as follows: $A_{n+1,i}=A_{i,n+1}=x_i$ and $A_{n+1,n+1}=scal$ .

bool	is_equal (Array1D< int > &a, Array1D< int > &b)
	Checks if two 1d int arrays are equal.

bool	is_equal (Array1D< double > &a, Array1D< double > &b)
	Checks if two 1d double arrays are equal.

bool	is_less (Array1D< int > &a, Array1D< int > &b)
	Checks if one 1d int array is less than another (by first element, then by second, etc...)

bool	is_less (Array1D< double > &a, Array1D< double > &b)
	Checks if one 1d double array is less than another (by first element, then by second, etc...)

int	vecIsInArray (Array1D< int > &vec, Array2D< int > &array)
	Checks if vec matches with any of the rows of array Returns the row number, or -1 if vec is not equal to any of the rows of array.

double	select_kth (int k, Array1D< double > &arr)
	Select the k-th smallest element of an array arr.

double	logdeterm (Array2D< double > &mat)
	Log-determinant of a real symmetric positive-definite matrix.

double	trace (Array2D< double > &mat)
	Trace of a matrix.

double	evalLogMVN (Array1D< double > &x, Array1D< double > &mu, Array2D< double > &Sigma)
	Evaluates the natural logarithm of a multivariate normal distribution.

Array2D< double >	diag (Array1D< double > &diagonal_array)
	Returns a diagonal matrix with a given diagonal.

Array1D< double >	copy (Array1D< double > &in_array)
	Returns a copy of 1D array.

Array2D< double >	copy (Array2D< double > &in_array)
	Return a copy of 2D Array.

Array2D< double >	mtxdel (Array2D< double > &A, int index, int dim)
	Deletes matrix columns or rows. Index specifies which column or row and dim = 1 deletes column, dim = 0 deletes the row.

Array1D< double >	add (Array1D< double > &x, Array1D< double > &y)
	Add two 1D Arrays and returns sum (must be of the same shape)

Array2D< double >	add (Array2D< double > &x, Array2D< double > &y)
	Add two 2D Arrays and returns sum (must be of same shape)

void	addinplace (Array2D< double > &x, Array2D< double > &y)
	Add two 2D Arrays in place. Summation is returned as x.

void	addinplace (Array1D< double > &x, Array1D< double > &y)
	Add two 1D Arrays in place. Summation is returned as x.

Array1D< double >	subtract (Array1D< double > &x, Array1D< double > &y)
	Returns subtraction of two 1D Arrays (must be of the same shape)

Array2D< double >	subtract (Array2D< double > &x, Array2D< double > &y)
	Returns subtraction of two 2D Arrays (must be of the same shape)

void	subtractinplace (Array2D< double > &x, Array2D< double > &y)
	Subtract two 2D Arrays in place. Difference is returned as x.

void	subtractinplace (Array1D< double > &x, Array1D< double > &y)
	Subtract two 1D Arrays in place. Difference is returned as x.

Array1D< double >	scale (Array1D< double > &x, double alpha)
	Returns 1D Arrays scaled by a double.

Array2D< double >	scale (Array2D< double > &x, double alpha)
	Returns 2D Array scaled by a double.

void	scaleinplace (Array1D< double > &x, double alpha)
	Multiply Array1D by double in place.

void	scaleinplace (Array1D< int > &x, int alpha)
	Multiply Array1D by int in place.

void	scaleinplace (Array2D< double > &x, double alpha)
	Multiply Array2D by double in place.

void	scaleinplace (Array2D< int > &x, int alpha)
	Multiply Array2D by int in place.

Array2D< double >	dotmult (Array2D< double > &A, Array2D< double > &B)
	Returns the elementwise multiplication of two 2D Arrays.

Array1D< double >	dotmult (Array1D< double > &A, Array1D< double > &B)
	Returns the elementwise multiplication of two 1D Arrays.

Array2D< double >	dotdivide (Array2D< double > &A, Array2D< double > &B)
	Returns the elementwise division of two 2D Arrays.

Array1D< double >	dotdivide (Array1D< double > &A, Array1D< double > &B)
	Returns the elementwise division of two 1D Arrays.

double	norm (Array1D< double > &x)
	Returns norm of 1D Array (Euclidean)

double	dist_sq (Array1D< double > &x, Array1D< double > &y, Array1D< double > &w)
	Weighted vector distance-squared.

Array2D< double >	Trans (Array2D< double > &A)
	Returns the transpose of a 2D Array.

double	dot (Array1D< double > &v1, Array1D< double > &v2)
	Returns the dot product of two 1D Arrays (must be of the same length)

Array1D< double >	dot (Array2D< double > &A, Array1D< double > &x)
	Returns the matrix vector product.

Array1D< double >	dot (Array1D< double > &x, Array2D< double > &A)

Array2D< double >	dot (Array2D< double > &A, Array2D< double > &B)
	Returns the matrix matrix product.

Array2D< double >	dotT (Array2D< double > &A, Array2D< double > &B)
	Returns the matrix matrix^T product.

Array2D< double >	INV (Array2D< double > &A)
	Returns the inverse of a square 2D Array.

Array2D< double >	AinvH (Array2D< double > &A, Array2D< double > &H)
	Solves linear system AX=H, i.e. returns A^(-1)*H, where A is real, symmetric and positive definite.

Array1D< double >	Ainvb (Array2D< double > &A, Array1D< double > &b)
	Solves linear system Ax=b, i.e. return A^(-1)*b where A is real, symmetric and positive definite.

void	LSTSQ (Array2D< double > &A, Array1D< double > &b, Array1D< double > &x)
	Least squares solution for overdetermined system. Note that A must be "taller than wide". Solution is returned in x.

void	QR (Array2D< double > &B, Array2D< double > &Q, Array2D< double > &R)
	Computes the QR factorization of a 2D Array (need not be square)

void	SVD (Array2D< double > &A, Array2D< double > &U, Array1D< double > &S, Array2D< double > &VT)
	Computes the SVD calculation of a 2D Array (need not be square)

void	printarray (Array1D< double > &x)
	Prints 1D double Array to screen (alternative to for loop using cout)

void	printarray (Array1D< int > &x)
	Prints 1D int Array to screen (alternative to for loop using cout)

void	printarray (Array2D< double > &x)
	Prints 2D double Array to screen (alternative to for loop using cout)

void	printarray (Array2D< int > &x)
	Prints 2D int Array to screen (alternative to for loop using cout)

Detailed Description

Tools to manipulate Array 1D and 2D objects. Some tools mimick MATLAB functionalities.

Function Documentation

◆ access()

double access	(	int	nx,
		int	ny,
		Array1D< double > &	arr_1,
		int	i,
		int	j )

Access element 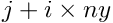$j+i\times ny$ from 1D array 'arr_1'.

◆ accessPythonHelper()

double accessPythonHelper	(	int	nx,
		int	ny,
		Array1D< double > &	arr_1,
		int	i,
		int	j )

Function written exclusively for Pybind11 to be able to load in the function access.

◆ add() [1/2]

Array1D< double > add	(	Array1D< double > &	x,
		Array1D< double > &	y )

Add two 1D Arrays and returns sum (must be of the same shape)

◆ add() [2/2]

Array2D< double > add	(	Array2D< double > &	x,
		Array2D< double > &	y )

Add two 2D Arrays and returns sum (must be of same shape)

◆ addinplace() [1/2]

void addinplace	(	Array1D< double > &	x,
		Array1D< double > &	y )

Add two 1D Arrays in place. Summation is returned as x.

◆ addinplace() [2/2]

void addinplace	(	Array2D< double > &	x,
		Array2D< double > &	y )

Add two 2D Arrays in place. Summation is returned as x.

◆ addVal() [1/9]

template void addVal	(	Array1D< double > &	arr1d,
		double	val )

◆ addVal() [2/9]

template void addVal	(	Array1D< int > &	arr1d,
		int	val )

◆ addVal() [3/9]

template<typename T >

void addVal	(	Array1D< T > &	arr1d,
		T	val )

Adds 'val' to all elements of 1D array arr1d (double or int)

◆ addVal() [4/9]

template void addVal	(	Array2D< double > &	arr2d,
		double	val )

◆ addVal() [5/9]

template void addVal	(	Array2D< int > &	arr2d,
		int	val )

◆ addVal() [6/9]

template<typename T >

void addVal	(	Array2D< T > &	arr2d,
		T	val )

Adds 'val' to all elements of 2D array arr2d (double or int)

◆ addVal() [7/9]

template void addVal	(	int	n,
		double *	arr1d,
		double	val )

◆ addVal() [8/9]

template void addVal	(	int	n,
		int *	arr1d,
		int	val )

◆ addVal() [9/9]

template<typename T >

void addVal	(	int	n,
		T *	arr1d,
		T	val )

Adds 'val' to the first n elements of an array pointer (double or int)

◆ addVecAlphaVecPow()

void addVec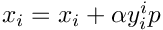AlphaVecPow	(	Array1D< double > &	x,
		double	alpha,
		Array1D< double > &	y,
		int	ip )

Implements $x_i=x_i+\alpha y_i^ip$ , where 'x' and 'y' are 1D arrays with $n$ elements.

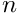
◆ Ainvb()

Array1D< double > Ainvb	(	Array2D< double > &	A,
		Array1D< double > &	b )

Solves linear system Ax=b, i.e. return A^(-1)*b where A is real, symmetric and positive definite.

◆ AinvH()

Array2D< double > AinvH	(	Array2D< double > &	A,
		Array2D< double > &	H )

Solves linear system AX=H, i.e. returns A^(-1)*H, where A is real, symmetric and positive definite.

◆ append() [1/2]

void append	(	Array1D< double > &	x,
		Array1D< double > &	y )

Append array y to array x in place (double format)

◆ append() [2/2]

void append	(	Array1D< int > &	x,
		Array1D< int > &	y )

Append array y to array x in place (int format)

◆ array1Dto2D() [1/3]

template void array1Dto2D	(	Array1D< double > &	arr_1d,
		Array2D< double > &	arr )

◆ array1Dto2D() [2/3]

template void array1Dto2D	(	Array1D< int > &	arr_1d,
		Array2D< int > &	arr )

◆ array1Dto2D() [3/3]

template<typename T >

void array1Dto2D	(	Array1D< T > &	arr_1d,
		Array2D< T > &	arr )

Store a given 1d array in a 2d array with a single second dimension.

◆ array2Dto1D() [1/3]

template void array2Dto1D	(	Array2D< double > &	arr_2d,
		Array1D< double > &	arr )

◆ array2Dto1D() [2/3]

template void array2Dto1D	(	Array2D< int > &	arr_2d,
		Array1D< int > &	arr )

◆ array2Dto1D() [3/3]

template<typename T >

void array2Dto1D	(	Array2D< T > &	arr_2d,
		Array1D< T > &	arr )

Store a given 2d array with a single second dimension in a 1d array.

◆ copy() [1/2]

Array1D< double > copy ( Array1D< double > & in_array )

Returns a copy of 1D array.

◆ copy() [2/2]

Array2D< double > copy ( Array2D< double > & in_array )

Return a copy of 2D Array.

◆ delCol() [1/6]

template void delCol	(	Array1D< double > &	x,
		int	icol )

◆ delCol() [2/6]

template void delCol	(	Array1D< int > &	x,
		int	icol )

◆ delCol() [3/6]

template<typename T >

void delCol	(	Array1D< T > &	x,
		int	icol )

Deletes element 'icol' from 1D array 'A'.

Todo: This should move to Array1D class

◆ delCol() [4/6]

template void delCol	(	Array2D< double > &	A,
		int	icol )

◆ delCol() [5/6]

template void delCol	(	Array2D< int > &	A,
		int	icol )

◆ delCol() [6/6]

template<typename T >

void delCol	(	Array2D< T > &	A,
		int	icol )

Deletes column 'icol' from 2D array 'A'.

Todo: This should move to Array2D class

◆ delRow() [1/3]

template void delRow	(	Array2D< double > &	A,
		int	irow )

◆ delRow() [2/3]

template void delRow	(	Array2D< int > &	A,
		int	irow )

◆ delRow() [3/3]

template<typename T >

void delRow	(	Array2D< T > &	A,
		int	irow )

Deletes row 'irow' from 2D array 'A'.

Todo: This should move to Array2D class

◆ diag()

Array2D< double > diag ( Array1D< double > & diagonal_array )

Returns a diagonal matrix with a given diagonal.

◆ dist_sq()

double dist_sq	(	Array1D< double > &	x,
		Array1D< double > &	y,
		Array1D< double > &	w )

Weighted vector distance-squared.

◆ dot() [1/4]

double dot	(	Array1D< double > &	v1,
		Array1D< double > &	v2 )

Returns the dot product of two 1D Arrays (must be of the same length)

◆ dot() [2/4]

Array1D< double > dot	(	Array1D< double > &	x,
		Array2D< double > &	A )

◆ dot() [3/4]

Array1D< double > dot	(	Array2D< double > &	A,
		Array1D< double > &	x )

Returns the matrix vector product.

◆ dot() [4/4]

Array2D< double > dot	(	Array2D< double > &	A,
		Array2D< double > &	B )

Returns the matrix matrix product.

◆ dotdivide() [1/2]

Array1D< double > dotdivide	(	Array1D< double > &	A,
		Array1D< double > &	B )

Returns the elementwise division of two 1D Arrays.

◆ dotdivide() [2/2]

Array2D< double > dotdivide	(	Array2D< double > &	A,
		Array2D< double > &	B )

Returns the elementwise division of two 2D Arrays.

◆ dotmult() [1/2]

Array1D< double > dotmult	(	Array1D< double > &	A,
		Array1D< double > &	B )

Returns the elementwise multiplication of two 1D Arrays.

◆ dotmult() [2/2]

Array2D< double > dotmult	(	Array2D< double > &	A,
		Array2D< double > &	B )

Returns the elementwise multiplication of two 2D Arrays.

◆ dotT()

Array2D< double > dotT	(	Array2D< double > &	A,
		Array2D< double > &	B )

Returns the matrix matrix^T product.

◆ evalLogMVN()

double evalLogMVN	(	Array1D< double > &	x,
		Array1D< double > &	mu,
		Array2D< double > &	Sigma )

Evaluates the natural logarithm of a multivariate normal distribution.

◆ find() [1/3]

template void find	(	Array1D< double > &	theta,
		double	lmbda,
		string	type,
		Array1D< int > &	indx )

◆ find() [2/3]

template void find	(	Array1D< int > &	theta,
		int	lmbda,
		string	type,
		Array1D< int > &	indx )

◆ find() [3/3]

template<typename T >

void find	(	Array1D< T > &	theta,
		T	lmbda,
		string	type,
		Array1D< int > &	indx )

Return list of indices corresponding to elements of 1D array theta that are: larger ( type="gt" ), larger or equal ( type="ge" ), smaller ( type="lt" ), smaller or equal ( type="le" ) than lmbda.

◆ flatten()

void flatten	(	Array2D< double > &	arr_2,
		Array1D< double > &	arr_1 )

Unfold/flatten a 2d array into a 1d array (double format)

◆ fold_1dto2d_colfirst()

void fold_1dto2d_colfirst	(	Array1D< double > &	x1,
		Array2D< double > &	x2 )

Fold a 1d array into a 2d array (double format), column first.

Note: The dimension of the 1d array needs to be equal to the product of the dimensions of the 2d array

◆ fold_1dto2d_rowfirst()

void fold_1dto2d_rowfirst	(	Array1D< double > &	x1,
		Array2D< double > &	x2 )

Fold a 1d array into a 2d array (double format), row first.

Note: The dimension of the 1d array needs to be equal to the product of the dimensions of the 2d array

◆ generate_multigrid() [1/3]

template void generate_multigrid	(	Array2D< double > &	multigrid,
		Array2D< double > &	grid )

◆ generate_multigrid() [2/3]

template void generate_multigrid	(	Array2D< int > &	multigrid,
		Array2D< int > &	grid )

◆ generate_multigrid() [3/3]

template<typename T >

void generate_multigrid	(	Array2D< T > &	multigrid,
		Array2D< T > &	grid )

Generates multigrid as a cartesian product of each column of grid.

Todo: Should ideally be written in a recursive manner, similar to computeMultiIndexTP() in tools/multiindex.cpp

◆ getCol() [1/3]

template void getCol	(	Array2D< double > &	arr2d,
		int	k,
		Array1D< double > &	arr1d )

◆ getCol() [2/3]

template void getCol	(	Array2D< int > &	arr2d,
		int	k,
		Array1D< int > &	arr1d )

◆ getCol() [3/3]

template<typename T >

void getCol	(	Array2D< T > &	arr2d,
		int	k,
		Array1D< T > &	arr1d )

Retrieves column 'k' from 2D array 'arr2d' and returns it in 1D array 'arr1d'.

◆ getRow() [1/3]

template void getRow	(	Array2D< double > &	arr2d,
		int	k,
		Array1D< double > &	arr1d )

◆ getRow() [2/3]

template void getRow	(	Array2D< int > &	arr2d,
		int	k,
		Array1D< int > &	arr1d )

◆ getRow() [3/3]

template<typename T >

void getRow	(	Array2D< T > &	arr2d,
		int	k,
		Array1D< T > &	arr1d )

Retrieves row 'k' from 2D array 'arr2d' and returns it in 1D array 'arr1d'.

◆ intersect() [1/2]

void intersect	(	Array1D< int > &	A,
		Array1D< int > &	B,
		Array1D< int > &	C )

Find common entries in 1D arrays 'A' and 'B' and return them in 'C', sorted in ascending order.

Note: Currently, duplicated entries in either 'A' and 'B' will be duplicated in 'C'

◆ intersect() [2/2]

void intersect	(	Array1D< int > &	A,
		Array1D< int > &	B,
		Array1D< int > &	C,
		Array1D< int > &	iA,
		Array1D< int > &	iB )

Finds common entries in 1D arrays 'A' and 'B' and returns them in 'C', sorted in ascending order. It also returns the original locations of these entries in 1D arrays 'iA' and 'iB', respectively.

Note: Currently, duplicated entries in either 'A' and 'B' will be duplicated in 'C'

◆ INV()

Array2D< double > INV ( Array2D< double > & A )

Returns the inverse of a square 2D Array.

◆ is_equal() [1/2]

bool is_equal	(	Array1D< double > &	a,
		Array1D< double > &	b )

Checks if two 1d double arrays are equal.

◆ is_equal() [2/2]

bool is_equal	(	Array1D< int > &	a,
		Array1D< int > &	b )

Checks if two 1d int arrays are equal.

◆ is_less() [1/2]

bool is_less	(	Array1D< double > &	a,
		Array1D< double > &	b )

Checks if one 1d double array is less than another (by first element, then by second, etc...)

◆ is_less() [2/2]

bool is_less	(	Array1D< int > &	a,
		Array1D< int > &	b )

Checks if one 1d int array is less than another (by first element, then by second, etc...)

◆ logdeterm()

double logdeterm ( Array2D< double > & mat )

Log-determinant of a real symmetric positive-definite matrix.

Todo: Check and catch the symmetric and positiv-definite conditions.

◆ LSTSQ()

void LSTSQ	(	Array2D< double > &	A,
		Array1D< double > &	b,
		Array1D< double > &	x )

Least squares solution for overdetermined system. Note that A must be "taller than wide". Solution is returned in x.

◆ matPvec() [1/3]

template void matPvec	(	Array2D< double > &	matrix,
		const Array1D< double > &	rc,
		double	alpha,
		char *	RC )

◆ matPvec() [2/3]

template void matPvec	(	Array2D< int > &	matrix,
		const Array1D< int > &	rc,
		int	alpha,
		char *	RC )

◆ matPvec() [3/3]

template<typename T >

void matPvec	(	Array2D< T > &	matrix,
		const Array1D< T > &	rc,
		T	alpha,
		char *	RC )

Adds scaled row or column to all rows / columns of a matrix (double or int)

Note: RC is a character "R" or "C" for row or column, correspondingly

◆ MatTMat()

Array2D< double > MatTMat ( Array2D< double > & A )

Returns $A^T A$ , where 'A' is a $\left[n\times k\right]$ 2D array.

◆ maxVal() [1/3]

template double maxVal	(	const Array1D< double > &	vector,
		int *	indx )

◆ maxVal() [2/3]

template int maxVal	(	const Array1D< int > &	vector,
		int *	indx )

◆ maxVal() [3/3]

template<typename T >

T maxVal	(	const Array1D< T > &	vector,
		int *	indx )

Returns maximum value in 'vector' and its location in *indx (double or int)

◆ merge() [1/3]

void merge	(	Array1D< double > &	x,
		Array1D< double > &	y,
		Array1D< double > &	xy )

Merge 1d double arrays.

◆ merge() [2/3]

void merge	(	Array1D< int > &	x,
		Array1D< int > &	y,
		Array1D< int > &	xy )

Merge 1d int arrays.

◆ merge() [3/3]

void merge	(	Array2D< double > &	x,
		Array2D< double > &	y,
		Array2D< double > &	xy )

Merge 2d double arrays (vertical stack)

◆ mtxdel()

Array2D< double > mtxdel	(	Array2D< double > &	A,
		int	index,
		int	dim )

Deletes matrix columns or rows. Index specifies which column or row and dim = 1 deletes column, dim = 0 deletes the row.

◆ norm()

double norm ( Array1D< double > & x )

Returns norm of 1D Array (Euclidean)

◆ paddMatCol() [1/2]

void paddMatCol	(	Array2D< double > &	A,
		Array1D< double > &	x )

Padds 2D array 'A' with the column 'x'.

Note: the number of elements in 'x' should be the same as the number of rows in 'A'

◆ paddMatCol() [2/2]

void paddMatCol	(	Array2D< int > &	A,
		Array1D< int > &	x )

Padds 2D array 'A' with the column 'x'.

Note: the number of elements in 'x' should be the same as the number of rows in 'A'

◆ paddMatColScal()

void paddMatColScal	(	Array2D< double > &	A,
		Array1D< double > &	x,
		double	scal )

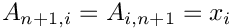
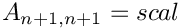
Padds square 2D array 'A' $\left[n\times n\right]$ with the elements of 'x' and 'scal' as follows: $A_{n+1,i}=A_{i,n+1}=x_i$ and $A_{n+1,n+1}=scal$ .

◆ paddMatRow() [1/2]

void paddMatRow	(	Array2D< double > &	A,
		Array1D< double > &	x )

Padds 2D array 'A' with the row 'x'.

Note: the number of elements in 'x' should be the same as the number of columns of 'A'

◆ paddMatRow() [2/2]

void paddMatRow	(	Array2D< int > &	A,
		Array1D< int > &	x )

Padds 2D array 'A' with the row 'x'.

Note: the number of elements in 'x' should be the same as the number of columns of 'A'

◆ paste() [1/4]

template void paste	(	Array1D< double > &	arr1,
		Array1D< double > &	arr2,
		Array2D< double > &	arr )

◆ paste() [2/4]

template void paste	(	Array1D< int > &	arr1,
		Array1D< int > &	arr2,
		Array2D< int > &	arr )

◆ paste() [3/4]

template<typename T >

void paste	(	Array1D< T > &	arr1,
		Array1D< T > &	arr2,
		Array2D< T > &	arr )

Paste two 1d arrays of same size into a single 2d array with second dimension equal to two.

◆ paste() [4/4]

void paste	(	Array2D< double > &	x,
		Array2D< double > &	y,
		Array2D< double > &	xy )

Paste two 2D arrays next to each other (horizontal stack)

◆ printarray() [1/4]

void printarray ( Array1D< double > & x )

Prints 1D double Array to screen (alternative to for loop using cout)

◆ printarray() [2/4]

void printarray ( Array1D< int > & x )

Prints 1D int Array to screen (alternative to for loop using cout)

◆ printarray() [3/4]

void printarray ( Array2D< double > & x )

Prints 2D double Array to screen (alternative to for loop using cout)

◆ printarray() [4/4]

void printarray ( Array2D< int > & x )

Prints 2D int Array to screen (alternative to for loop using cout)

◆ prod_vecTmatvec()

double prod_vecTmatvec	(	Array1D< double > &	a,
		Array2D< double > &	B,
		Array1D< double > &	c )

Returns $a^T B c$ .

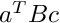
◆ prodAlphaMatMat()

void prodAlphaMatMat	(	Array2D< double > &	A,
		Array2D< double > &	B,
		double	alpha,
		Array2D< double > &	C )

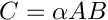
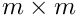
Returns $C=\alpha AB$ , where 'A' and 'B' are $\left[m\times n\right]$ 2D arrays and 'alpha' is a scalar. The 2D array 'C' has $m\times m$ elements.

◆ prodAlphaMatTMat()

void prodAlphaMatTMat	(	Array2D< double > &	A,
		Array2D< double > &	B,
		double	alpha,
		Array2D< double > &	C )

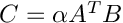
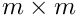
Returns $C=\alpha A^TB$ , where 'A' and 'B' are $\left[m\times n\right]$ 2D arrays and 'alpha' is a scalar. The 2D array 'C' has $m\times m$ elements.

◆ prodAlphaMatTVec()

void prodAlphaMatTVec	(	Array2D< double > &	A,
		Array1D< double > &	x,
		double	alpha,
		Array1D< double > &	y )

Returns 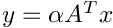$y=\alpha A^Tx$ , where 'A' is a $\left[m\times n\right]$ 2D array, 'x' is 1D array of size $m$ and 'alpha' is a scalar. The 1D array 'y' has $n$ elements.

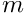
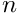
◆ prodAlphaMatVec()

void prodAlphaMatVec	(	Array2D< double > &	A,
		Array1D< double > &	x,
		double	alpha,
		Array1D< double > &	y )

Returns 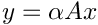$y=\alpha Ax$ , where 'A' is a $\left[n\times m\right]$ 2D array, 'x' is 1D array of size $m$ and 'alpha' is a scalar. The 1D array 'y' has $n$ elements.

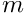
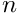
◆ QR()

void QR	(	Array2D< double > &	B,
		Array2D< double > &	Q,
		Array2D< double > &	R )

Computes the QR factorization of a 2D Array (need not be square)

◆ quicksort3() [1/3]

void quicksort3	(	Array1D< double > &	arr,
		int	l,
		int	r )

Quick-sort with 3-way partitioning of array between indices l and r.

◆ quicksort3() [2/3]

void quicksort3	(	Array2D< double > &	arr,
		int	l,
		int	r )

Quick-sort with 3-way partitioning of 2d array between indices l and r, and sorting is done comparing rows (by first element, then by second, etc...)

◆ quicksort3() [3/3]

void quicksort3	(	Array2D< double > &	arr,
		int	l,
		int	r,
		int	col )

Quick-sort with 3-way partitioning of 2d array between indices l and r, according to column col.

◆ scale() [1/2]

Array1D< double > scale	(	Array1D< double > &	x,
		double	alpha )

Returns 1D Arrays scaled by a double.

◆ scale() [2/2]

Array2D< double > scale	(	Array2D< double > &	x,
		double	alpha )

Returns 2D Array scaled by a double.

◆ scaleinplace() [1/4]

void scaleinplace	(	Array1D< double > &	x,
		double	alpha )

Multiply Array1D by double in place.

◆ scaleinplace() [2/4]

void scaleinplace	(	Array1D< int > &	x,
		int	alpha )

Multiply Array1D by int in place.

◆ scaleinplace() [3/4]

void scaleinplace	(	Array2D< double > &	x,
		double	alpha )

Multiply Array2D by double in place.

◆ scaleinplace() [4/4]

void scaleinplace	(	Array2D< int > &	x,
		int	alpha )

Multiply Array2D by int in place.

◆ select_kth()

double select_kth	(	int	k,
		Array1D< double > &	arr )

Select the k-th smallest element of an array arr.

◆ setdiff()

void setdiff	(	Array1D< int > &	A,
		Array1D< int > &	B,
		Array1D< int > &	C )

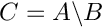
Returns $C=A\backslash B$ (C=Elements of A that are not in B); C is sorted in ascending order.

◆ setdiff_s()

void setdiff_s	(	Array1D< int > &	A,
		Array1D< int > &	B,
		Array1D< int > &	C )

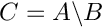
Returns $C=A\backslash B$ ( C=Elements of A that are not in B); C is sorted in ascending order.

Note: Assumes A is sorted and uses a faster algorithm than setdiff

Todo: In future, this should sort A too and replace setdiff

Note: B is sorted on output as well

◆ shell_sort() [1/3]

void shell_sort ( Array1D< double > & array )

Sorts double array in ascending order.

◆ shell_sort() [2/3]

void shell_sort ( Array1D< int > & array )

Sorts integer array in ascending order.

◆ shell_sort() [3/3]

void shell_sort	(	int *	a,
		int	n )

Sorts integer array.

◆ shell_sort_all()

void shell_sort_all	(	Array2D< double > &	array,
		Array1D< int > &	newInd,
		Array1D< int > &	oldInd )

Sorts double array in ascending order according to first column, then second column breaks the tie, and so on.

◆ shell_sort_col()

void shell_sort_col	(	Array2D< double > &	array,
		int	col,
		Array1D< int > &	newInd,
		Array1D< int > &	oldInd )

Sorts double array in ascending order according to a given column.

◆ subMatrix_col() [1/3]

template void subMatrix_col	(	Array2D< double > &	matrix,
		Array1D< int > &	ind,
		Array2D< double > &	submatrix )

◆ subMatrix_col() [2/3]

template void subMatrix_col	(	Array2D< int > &	matrix,
		Array1D< int > &	ind,
		Array2D< int > &	submatrix )

◆ subMatrix_col() [3/3]

template<typename T >

void subMatrix_col	(	Array2D< T > &	matrix,
		Array1D< int > &	ind,
		Array2D< T > &	submatrix )

Extracts from 'matrix' columns corresponding to indices 'ind' and returns them in 'submatrix' (double or int)

◆ subMatrix_row() [1/3]

template void subMatrix_row	(	Array2D< double > &	matrix,
		Array1D< int > &	ind,
		Array2D< double > &	submatrix )

◆ subMatrix_row() [2/3]

template void subMatrix_row	(	Array2D< int > &	matrix,
		Array1D< int > &	ind,
		Array2D< int > &	submatrix )

◆ subMatrix_row() [3/3]

template<typename T >

void subMatrix_row	(	Array2D< T > &	matrix,
		Array1D< int > &	ind,
		Array2D< T > &	submatrix )

Extracts from 'matrix' rows corresponding to indices 'ind' and returns them in 'submatrix' (double or int)

◆ subtract() [1/2]

Array1D< double > subtract	(	Array1D< double > &	x,
		Array1D< double > &	y )

Returns subtraction of two 1D Arrays (must be of the same shape)

◆ subtract() [2/2]

Array2D< double > subtract	(	Array2D< double > &	x,
		Array2D< double > &	y )

Returns subtraction of two 2D Arrays (must be of the same shape)

◆ subtractinplace() [1/2]

void subtractinplace	(	Array1D< double > &	x,
		Array1D< double > &	y )

Subtract two 1D Arrays in place. Difference is returned as x.

◆ subtractinplace() [2/2]

void subtractinplace	(	Array2D< double > &	x,
		Array2D< double > &	y )

Subtract two 2D Arrays in place. Difference is returned as x.

◆ subVector() [1/3]

template void subVector	(	Array1D< double > &	vector,
		Array1D< int > &	ind,
		Array1D< double > &	subvector )

◆ subVector() [2/3]

template void subVector	(	Array1D< int > &	vector,
		Array1D< int > &	ind,
		Array1D< int > &	subvector )

◆ subVector() [3/3]

template<typename T >

void subVector	(	Array1D< T > &	vector,
		Array1D< int > &	ind,
		Array1D< T > &	subvector )

Extracts from 'vector', elements corresponding to indices 'ind' and returns them in 'subvector' (double or int)

◆ SVD()

void SVD	(	Array2D< double > &	A,
		Array2D< double > &	U,
		Array1D< double > &	S,
		Array2D< double > &	VT )

Computes the SVD calculation of a 2D Array (need not be square)

◆ swap() [1/2]

void swap	(	Array1D< double > &	arr,
		int	i,
		int	j )

Swap i-th and j-th elements of the array arr.

◆ swap() [2/2]

void swap	(	Array2D< double > &	arr,
		int	i,
		int	j )

Swap i-th and j-th rows of the 2d array arr.

◆ trace()

double trace ( Array2D< double > & mat )

Trace of a matrix.

◆ Trans()

Array2D< double > Trans ( Array2D< double > & A )

Returns the transpose of a 2D Array.

◆ transpose() [1/3]

template void transpose	(	Array2D< double > &	x,
		Array2D< double > &	xt )

◆ transpose() [2/3]

template void transpose	(	Array2D< int > &	x,
		Array2D< int > &	xt )

◆ transpose() [3/3]

template<typename T >

void transpose	(	Array2D< T > &	x,
		Array2D< T > &	xt )

Transpose a 2d double or int array x and return the result in xt.

◆ vecIsInArray()

int vecIsInArray	(	Array1D< int > &	vec,
		Array2D< int > &	array )

Checks if vec matches with any of the rows of array Returns the row number, or -1 if vec is not equal to any of the rows of array.

Functions

Detailed Description

Function Documentation

◆ access()

◆ accessPythonHelper()

◆ add() [1/2]

◆ add() [2/2]

◆ addinplace() [1/2]

◆ addinplace() [2/2]

◆ addVal() [1/9]

◆ addVal() [2/9]

◆ addVal() [3/9]

◆ addVal() [4/9]

◆ addVal() [5/9]

◆ addVal() [6/9]

◆ addVal() [7/9]

◆ addVal() [8/9]

◆ addVal() [9/9]

◆ addVecAlphaVecPow()

◆ Ainvb()

◆ AinvH()

◆ append() [1/2]

◆ append() [2/2]

◆ array1Dto2D() [1/3]

◆ array1Dto2D() [2/3]

◆ array1Dto2D() [3/3]

◆ array2Dto1D() [1/3]

◆ array2Dto1D() [2/3]

◆ array2Dto1D() [3/3]

◆ copy() [1/2]

◆ copy() [2/2]

◆ delCol() [1/6]

◆ delCol() [2/6]

◆ delCol() [3/6]

◆ delCol() [4/6]

◆ delCol() [5/6]

◆ delCol() [6/6]

◆ delRow() [1/3]

◆ delRow() [2/3]

◆ delRow() [3/3]

◆ diag()

◆ dist_sq()

◆ dot() [1/4]

◆ dot() [2/4]

◆ dot() [3/4]

◆ dot() [4/4]

◆ dotdivide() [1/2]

◆ dotdivide() [2/2]

◆ dotmult() [1/2]

◆ dotmult() [2/2]

◆ dotT()

◆ evalLogMVN()

◆ find() [1/3]

◆ find() [2/3]

◆ find() [3/3]

◆ flatten()

◆ fold_1dto2d_colfirst()

◆ fold_1dto2d_rowfirst()

◆ generate_multigrid() [1/3]

◆ generate_multigrid() [2/3]

◆ generate_multigrid() [3/3]

◆ getCol() [1/3]

◆ getCol() [2/3]

◆ getCol() [3/3]

◆ getRow() [1/3]

◆ getRow() [2/3]

◆ getRow() [3/3]

◆ intersect() [1/2]

◆ intersect() [2/2]

◆ INV()

◆ is_equal() [1/2]

◆ is_equal() [2/2]

◆ is_less() [1/2]

◆ is_less() [2/2]

◆ logdeterm()

◆ LSTSQ()

◆ matPvec() [1/3]

◆ matPvec() [2/3]

◆ matPvec() [3/3]

◆ MatTMat()