Axioms for the theory of proveit.logic.sets.inclusion

import proveit
# Prepare this notebook for defining the axioms of a theory:
%axioms_notebook # Keep this at the top following 'import proveit'.
from proveit.logic import SetNotEquiv, SubsetEq, NotSubsetEq, ProperSubset, NotProperSubset
from proveit.logic import Forall, Equals, And, InSet, Not
from proveit import A, B, x
%begin axioms

Defining axioms for theory 'proveit.logic.sets.inclusion'
Subsequent end-of-cell assignments will define axioms
%end_axioms will finalize the definitions

$A \subseteq B$ is equivalent to saying that every element in $A$ is also in $B$:

subset_eq_def = Forall((A, B), Equals(SubsetEq(A, B), Forall(x, InSet(x, B), domain=A)))

subset_eq_def:

Define $A \nsubseteq B$ as $\lnot (A \subseteq B)$:

not_subset_eq_def = Forall((A, B), Equals(NotSubsetEq(A, B), Not(SubsetEq(A, B))))

not_subset_eq_def:

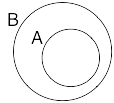
$A$ is a proper subset of $B$, $A \subset B$, means that $A \subseteq B$ but $B \nsubseteq A$; that is, every element in $A$ is also in $B$ but not the other way around (i.e. there are elements in $B$ that are not in $A$):

proper_subset_def = Forall((A, B), Equals(ProperSubset(A, B), And(SubsetEq(A, B), SetNotEquiv(B, A))))

proper_subset_def:

not_proper_subset_def = Forall((A, B), Equals(NotProperSubset(A, B), Not(ProperSubset(A, B))))

not_proper_subset_def:

%end axioms

These axioms may now be imported from the theory package: proveit.logic.sets.inclusion