Ctrl+K

Exercise 4: Quantifying probability of detection

Exercise 4: Quantifying probability of detection#


Goal#

Understand how MAPIT can be used to evaluate probability of detection. So far, exercises have focused on exploring qualitative changes that are induced by changes in measurement uncertainty or material loss. This section will focus on developing quantitative metrics for safeguards performance.

Caution

This exercise assumes that you are familiar with MAPIT and can perform tasks discussed in the previous exercises; exercise 1, exercise 2 and exercise 3.

Problem setup#

  • Start this exercise by launching MAPIT, selecting the Normal dataset.

    • This tutorial starts by assuming you are at the main MAPIT interface

  • Select all the checkboxes for available statistical tests

    • A total of five (5) checkboxes should be checked

      • MUF

      • Cumulative MUF

      • Sigma MUF

      • SITMUF

      • Page’s test on SITMUF

  • Next, configure the required parameters in the statistical box using the same parameters from exercise 1 and 2:

    • MBP: 416

    • Iterations: 50

      • If running on a lower performance device, try running with Iterations: 20

    • Analysis Element/Index: U

    • Temporal Offset : Empty

  • Set the measurement errors by pressing the Select Errors button. Choose 0.5% for all random and systematic errors.

  • Run MAPIT by pressing the Run button.

Note

Safeguards statistical tests are commonly tuned to have an average false alarm probability of 5% per year. The next steps will use MAPIT functionality to determine this threshold for Page’s trend test on SITMUF.

Caution

The data provided in these examples are 6480 hours long, which translate to about 270 days (a reasonable estimate of an operational year). Therefore, one iteration is a single year of simulated operation. When using your own data, use caution in determining statistical thresholds if your datasets have different lengths of time.

Determining statistical thresholds#

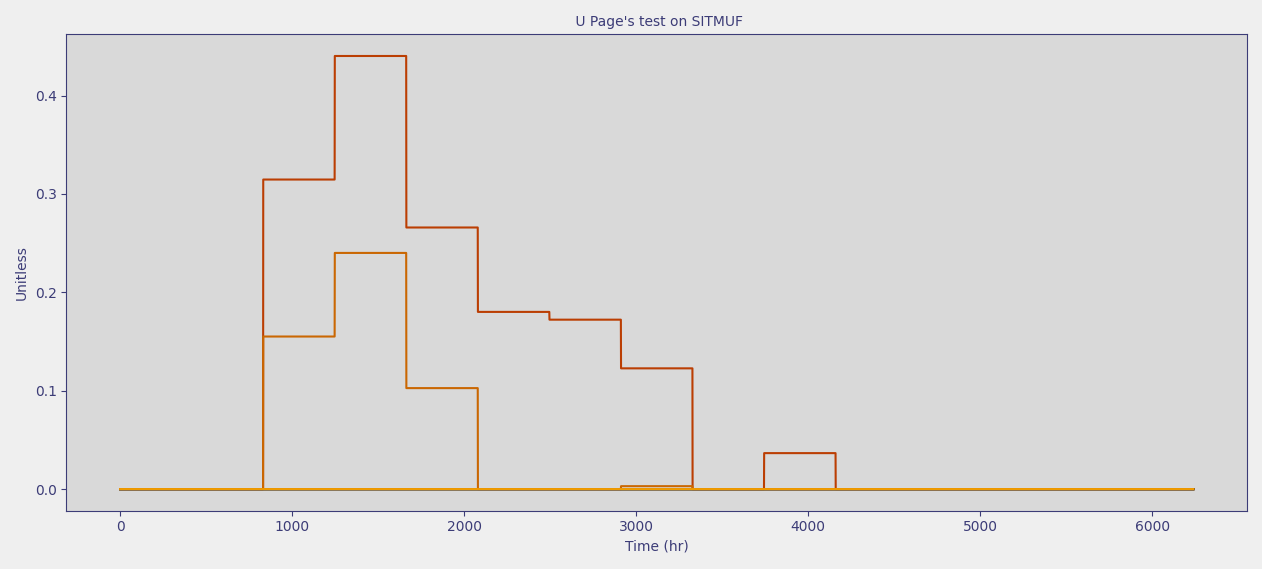
  • Plot Page’s trend test on SITMUF

    • This is labeled as U Page's test on SITMUF in MAPIT

    • Plotting a quantity is necessary to use the threshold functionality

Note

Plots in this excercise are using 300 iterations to have better statistics, so if less iterations are being run the results may differ slightly from those shown here. In large iteration datasets, MAPIT only plots 15 iterations to ensure the plotting window is not overloaded.

_images/PageUSITMUF1.png

  • Use the Statistical Thresholds box to determine an appropriate threshold (i.e. 5% FAP)

    • This is performed by entering values in the Enter Threshold box

    • MAPIT returns the number of iterations that exceed this threshold

      • MAPIT operates on the entire dataset, not just the iterations that are plotted. This can be important in cases where many iterations are calculated and only a few are plotted.

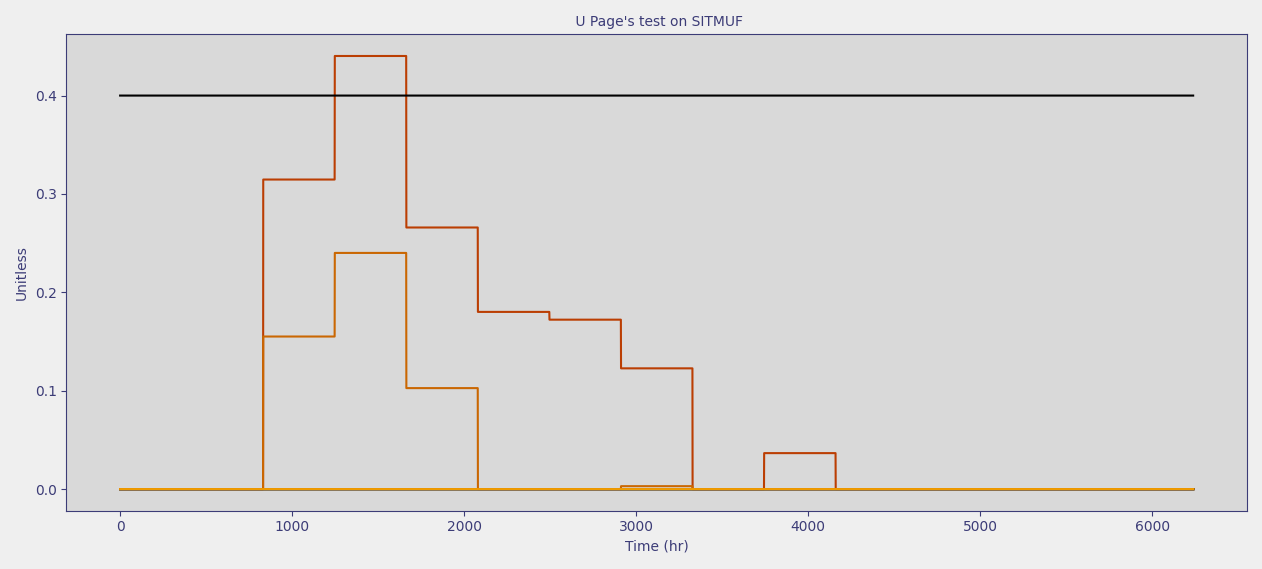
_images/PageUSITMUF2.png

  • Your threshold should be near 0.5

    • Due to the randomness of the calculations, your threshold might be slightly different

    • Increasing the number of iterations can help obtain a more precise estimate of the threshold

      • The uncertainty in the threshold itself should roughly decrease with sqrt(iterations).

Evaluating probability of detection#

  • Load the Abrupt dataset.

  • Select the same options from steps 2, 3, and 4 then run MAPIT.

    • Select all the options in the Tests/Uranium box

    • Select a value of 0.5% for all random and systematic errors

    • MBP: 416

    • Iterations: 50

      • If running on a lower performance device, try running with Iterations: 20

    • Analysis Element/Index: U

    • Temporal Offset = empty: Empty

  • Plot Page’s trend test on U SITMUF

    • This is labeled as U Page's test on SITMUF in MAPIT

_images/PageUSITMUF3.png

  • Enter in the previously determined threshold to determine the probability of detection for this material loss.

    • The value should be approximately 50-60%

Note

In this exercise, we changed the measurement uncertainties for all locations to be the same value. However, in practice, different measurement technologies are deployed based on safeguards need. On your own, try changing just some high impact measurement locations to 0.5% while leaving others at higher levels to see if you can reach similar results.

Summary#

🎉 You have finished the fourth MAPIT exercise. 🎉

This exercise introduced the the SITMUF test in MAPIT along with the capability to set threshold and evaluate probability of detection. In this exercise you:

  • Set a threshold based on a false alarm probability

  • Evaluated probabilities of detection

  • Explored the SITMUF transform

  • Explored Page’s trend test on SITMUF

For an optional challenge, continue to exercise 5.

Contents